
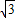 .
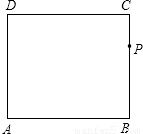
.
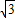 ,根据反三角函数,可知∠AED=60°,同理可知∠CEB=60°,从而求出∠AEB=∠CEB=60°,即EB平分∠AEC.
,根据反三角函数,可知∠AED=60°,同理可知∠CEB=60°,从而求出∠AEB=∠CEB=60°,即EB平分∠AEC.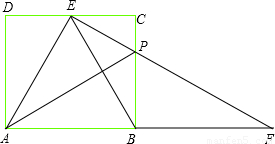 解:(1)当E为CD中点时,EB平分∠AEC,
解:(1)当E为CD中点时,EB平分∠AEC,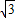 ,
,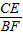 =
=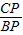 =
= ,
,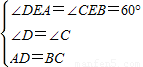 ,
,
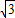 ,CE=1,∠C=90°,
,CE=1,∠C=90°,
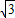 .
.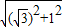 =2,
=2,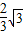 ,
,

科目:初中数学 来源:2011年重庆市綦江县中考数学模拟试卷(解析版) 题型:解答题
 .
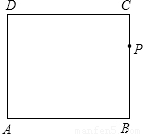
.
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《图形的相似》(02)(解析版) 题型:填空题
查看答案和解析>>
科目:初中数学 来源:2008年全国中考数学试题汇编《图形认识初步》(03)(解析版) 题型:解答题
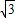 .
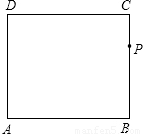
.
查看答案和解析>>
科目:初中数学 来源:2008年江苏省泰州市中考数学试卷(解析版) 题型:选择题
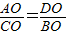 ;(4)∠OAD=∠OBC.若只增加其中的一个条件,就一定能使∠BAC=∠CDB成立,这样的条件可以是( )
;(4)∠OAD=∠OBC.若只增加其中的一个条件,就一定能使∠BAC=∠CDB成立,这样的条件可以是( )查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com