
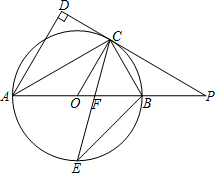
 如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.
如图,AB是⊙O的直径,点C是⊙O上一点,AD与过点C的切线垂直,垂足为点D,直线DC与AB的延长线相交于点P,弦CE平分∠ACB,交AB于点F,连接BE.分析 (1)由切线得:OC⊥PC,再得平行,由同圆的半径相等:OA=OC,根据等边对等角可得结论;
(2)证明∠PFC=∠PCF,根据等角对等边可得结论;
(3)作辅助线,构建直角三角形,根据三角函数的比设未知数,利用勾股定理列方程可得结论.
解答 证明:(1)∵PC为⊙O的切线,
∴OC⊥PC,
∵AD⊥PC,
∴AD∥OC,
∴∠DAC=∠ACO,
∵OA=OC,
∴∠OAC=∠ACO,
∴∠DAC=∠OAC,
∴AC平分∠DAB;
(2)∵CE平分∠ACB,
∴∠ACE=∠BCE,
∴$\widehat{AE}$=$\widehat{BE}$,
∴∠ABE=∠ECB,
∵∠BCP+∠OCB=∠BCP+∠OBC=∠BAC+∠OBC=90°,
∴∠BCP=∠BAC,
∵∠BAC=∠BEC,
∴∠BCP=∠BEC,
∵∠PFC=∠BEC+∠ABE,
∠PCF=∠ECB+∠BCP,
∴∠PFC=∠PCF,
∴PC=PF;
(3)连接AE.
∵$\widehat{AE}$=$\widehat{BE}$,
∴AE=BE,
又∵AB是直径,
∴∠AEB=90°,
AB=$\sqrt{2}$BE=$\sqrt{2}$×$7\sqrt{2}$=14,
∴OB=OC=7,
∵∠PCB=∠PAC,∠P=∠P,
∴△PCB∽△PAC,
∴$\frac{PB}{PC}=\frac{BC}{AC}$,
∵tan∠ABC=$\frac{4}{3}=\frac{AC}{BC}$,
∴$\frac{PB}{PC}$=$\frac{3}{4}$,
设PB=3x,则PC=4x,
在Rt△POC中,(3x+7)2=(4x)2+72,
解得x1=0(舍),x2=6,
∵x>0,
∴x=6,
∴PC=4x=4×6=24.
点评 本题考查了圆的切线性质,及解直角三角形的知识.运用切线的性质来进行计算或论证,常通过三角函数的比设未知数,表示线段的长,利用垂直构造直角三角形,根据勾股定理列方程解决有关问题.


 阳光课堂同步练习系列答案
阳光课堂同步练习系列答案科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
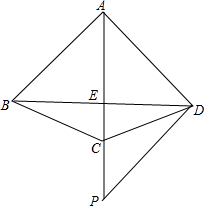 如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.
如图,四边形ABCD中,AB=AC=AD,AC平分∠BAD,点P是AC延长线上一点,且PD⊥AD.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
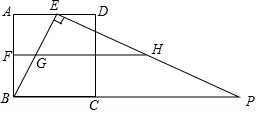 如图,正方形ABCD的边长为4,点E、F分别是边AD、AB的中点,点P是BC延长线上一点,且EP⊥EB,过点F作FH∥BP,分别交EB、EP于G、H两点,将△EGH绕点E逆时针旋转α(0°<α<90°),得到△EMN(M、N分别是G、H的对应点),使直线MN恰好经过点B.
如图,正方形ABCD的边长为4,点E、F分别是边AD、AB的中点,点P是BC延长线上一点,且EP⊥EB,过点F作FH∥BP,分别交EB、EP于G、H两点,将△EGH绕点E逆时针旋转α(0°<α<90°),得到△EMN(M、N分别是G、H的对应点),使直线MN恰好经过点B.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
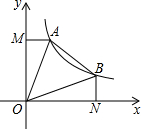 如图,一次函数y=-x+b(b>0)的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,连接OA、OB,AM⊥y轴,BN⊥x轴,垂足分别为M、N.下列结论:
如图,一次函数y=-x+b(b>0)的图象与反比例函数y=$\frac{k}{x}$(x>0)的图象交于A、B两点,连接OA、OB,AM⊥y轴,BN⊥x轴,垂足分别为M、N.下列结论:| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
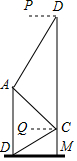 如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).
如图,某中学在教学楼前新建了一座雕塑AB,为了测量雕塑的高度,小明在二楼找到一点C,利用三角尺测得雕塑顶端点A的仰角∠QCA为45°,底部点B的俯角∠QCB为30°,小华在五楼找到一点D,利用三角尺测得点A的俯角∠PDA为60°,若AD为8m,则雕塑AB的高度为多少?(结果精确到0.1m,参考数据:$\sqrt{3}$≈1.73).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
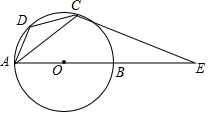 如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.
如图,AB为⊙O的直径,AD为弦,过⊙O上一点C作⊙O的切线交AB的延长线于E,且∠DCA=∠E.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com