
Ζ÷Έω Θ®1Θ©Ιέ≤λΗχΕ®Β» ΫΘ§ΗυΨίΒ» ΫΒΡ±δΜ·’“≥ω±δΜ·Ιφ¬…ΓΑ$\frac{1}{nΘ®n+1Θ©}$=$\frac{1}{n}$-$\frac{1}{n+1}$Θ®nΈΣ’ϊ ΐΘ§«“nΓΌ0ΚΆ-1Θ©Γ±ΘΜ
Θ®2Θ©“‘ΦΑΘ®1Θ©ΒΟ≥ωΒΡΙφ¬…Φ¥Ω…ΒΟ≥ωΫα¬έΘ°
Ϋβ¥π ΫβΘΚΘ®1Θ©Ιέ≤λΘ§ΖΔœ÷Ιφ¬…ΘΚ$\frac{1}{2ΓΝ3}$=$\frac{1}{2}-\frac{1}{3}$Θ§$\frac{1}{3ΓΝ4}$=$\frac{1}{3}-\frac{1}{4}$Θ§$\frac{1}{4ΓΝ5}$=$\frac{1}{4}-\frac{1}{5}$Θ§$\frac{1}{5ΓΝ6}$=$\frac{1}{5}$-$\frac{1}{6}$Θ§Γ≠Θ§
Γύ$\frac{1}{nΘ®n+1Θ©}$=$\frac{1}{n}$-$\frac{1}{n+1}$Θ®nΈΣ’ϊ ΐΘ§«“nΓΌ0ΚΆ-1Θ©Θ°
Θ®2Θ©ΫαΚœΘ®1Θ©ΒΡΫα¬έΩ…÷ΣΘΚ
‘≠ Ϋ=$\frac{1}{x-2}-\frac{1}{x-1}$+$\frac{1}{x-3}-\frac{1}{x-2}$+$\frac{1}{x-4}-\frac{1}{x-3}$Θ§
=$\frac{1}{x-4}-\frac{1}{x-1}$Θ§
=$\frac{3}{Θ®x-4Θ©Θ®x-1Θ©}$Θ°
ΒψΤά ±ΨΧβΩΦ≤ιΝΥΙφ¬…–Ά÷–ΒΡ ΐΉ÷ΒΡ±δΜ·άύΘ§ΫβΧβΒΡΙΊΦϋ «’“≥ω±δΜ·Ιφ¬…ΓΑ$\frac{1}{nΘ®n+1Θ©}$=$\frac{1}{n}$-$\frac{1}{n+1}$Θ®nΈΣ’ϊ ΐΘ§«“nΓΌ0ΚΆ-1Θ©Γ±Θ°±ΨΧβ τ”ΎΜυ¥ΓΧβΘ§Ρ―Ε»≤Μ¥σΘ§ΫβΨωΗΟΧβ–ΆΧβΡΩ ±Θ§ΗυΨίΒ» ΫΒΡ±δΜ·’“≥ω±δΜ·Ιφ¬… «ΙΊΦϋΘ°



| ΡξΦΕ | ΗΏ÷–ΩΈ≥Χ | ΡξΦΕ | ≥θ÷–ΩΈ≥Χ |
| ΗΏ“Μ | ΗΏ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ“Μ | ≥θ“ΜΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏΕΰ | ΗΏΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θΕΰ | ≥θΕΰΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
| ΗΏ»ΐ | ΗΏ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ | ≥θ»ΐ | ≥θ»ΐΟβΖ―ΩΈ≥ΧΆΤΦωΘΓ |
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
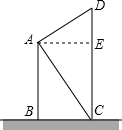 –ΓΜΣΦ“”κ–ΓάωΦ“ΒΡΝΫ¬ΞœύΝΎΘ§«“œύΨύ10ΟΉΘ§»γΆΦΘ§–ΓΜΣΦ“ΒΡ¬ΞΗΏABΈΣ18ΟΉΘΜ¥”–ΓΜΣΦ“¬ΞΒΡΕΞ≤ΩΡΩ≤β–ΓάωΦ“ΉΓΒΡ¬ΞΖΩCDΒΡΒΉ≤Ω”κΕΞ≤ΩΘ§ ”œΏ”κΥ°ΤΫœΏΒΡΦ–Ϋ«Ζ÷±πΈΣ55ΓψΚΆ35ΓψΘ§ΡψΡήΖώ«σ≥ω–ΓάωΦ“ΉΓΒΡ¬ΞΖΩCD”–ΕύΗΏΘΩ«κΥΒΟςάμ”…Θ°
–ΓΜΣΦ“”κ–ΓάωΦ“ΒΡΝΫ¬ΞœύΝΎΘ§«“œύΨύ10ΟΉΘ§»γΆΦΘ§–ΓΜΣΦ“ΒΡ¬ΞΗΏABΈΣ18ΟΉΘΜ¥”–ΓΜΣΦ“¬ΞΒΡΕΞ≤ΩΡΩ≤β–ΓάωΦ“ΉΓΒΡ¬ΞΖΩCDΒΡΒΉ≤Ω”κΕΞ≤ΩΘ§ ”œΏ”κΥ°ΤΫœΏΒΡΦ–Ϋ«Ζ÷±πΈΣ55ΓψΚΆ35ΓψΘ§ΡψΡήΖώ«σ≥ω–ΓάωΦ“ΉΓΒΡ¬ΞΖΩCD”–ΕύΗΏΘΩ«κΥΒΟςάμ”…Θ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΧνΩ’Χβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
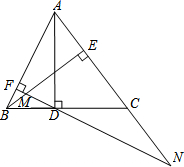 »γΆΦΘ§ADΓΔBE «ΓςABCΒΡΝΫΧθΗΏΘ§ΙΐΒψDΉςDFΓΆABΘ§¥ΙΉψΈΣFΘ§FDΫΜBE”ΎMΘ§FDΓΔACΒΡ―”≥ΛœΏΫΜ”ΎΒψNΘ°
»γΆΦΘ§ADΓΔBE «ΓςABCΒΡΝΫΧθΗΏΘ§ΙΐΒψDΉςDFΓΆABΘ§¥ΙΉψΈΣFΘ§FDΫΜBE”ΎMΘ§FDΓΔACΒΡ―”≥ΛœΏΫΜ”ΎΒψNΘ°≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚΫβ¥πΧβ
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΩΤΡΩΘΚ≥θ÷– ΐ―ß ά¥‘¥ΘΚ Χβ–ΆΘΚ―Γ‘ώΧβ
| AΘ° | 3a+2b=5ab | BΘ° | 2a3+3a2=5a5 | CΘ° | 5a2-4a2=1 | DΘ° | 5a2b-5ba2=0 |
≤ιΩ¥¥πΑΗΚΆΫβΈω>>
ΑΌΕ»÷¬–≈ - ΝΖœΑ≤αΝ–±μ - ‘ΧβΝ–±μ
Κΰ±± ΓΜΞΝΣΆχΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΤΫΧ® | Άχ…œ”–ΚΠ–≈œΔΨΌ±®Ή®«χ | Βγ–≈’©Τ≠ΨΌ±®Ή®«χ | …φάζ Ζ–ιΈό÷ς“ε”–ΚΠ–≈œΔΨΌ±®Ή®«χ | …φΤσ«÷»®ΨΌ±®Ή®«χ
ΈΞΖ®ΚΆ≤ΜΝΦ–≈œΔΨΌ±®ΒγΜΑΘΚ027-86699610 ΨΌ±®” œδΘΚ58377363@163.com