
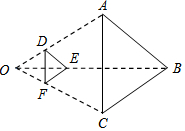
 如图,以点O为位似中心,将△ABC缩小后得到△DEF,已知OD=1,OA=3.若△DEF的面积为S,则△ABC的面积为( )
如图,以点O为位似中心,将△ABC缩小后得到△DEF,已知OD=1,OA=3.若△DEF的面积为S,则△ABC的面积为( )| A. | 2S | B. | 3S | C. | 4S | D. | 9S |
分析 利用位似的性质和相似三角形的性质得到$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{OD}{OA}$)2,然后利用比例性质可求出△ABC的面积.
解答 解:∵△ABC与△DEF位似,
∴$\frac{{S}_{△DEF}}{{S}_{△ABC}}$=($\frac{OD}{OA}$)2=$\frac{1}{9}$,
∴△ABC的面积=9S.
故选D.
点评 本题考查了位似变换:如果两个图形不仅是相似图形,而且对应顶点的连线相交于一点,对应边互相平行,那么这样的两个图形叫做位似图形,这个点叫做位似中心.注意:①两个图形必须是相似形;②对应点的连线都经过同一点;③对应边平行.


科目:初中数学 来源: 题型:解答题
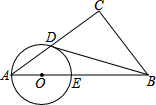 已知:如图所示,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A,求证:BD与⊙O相切.
已知:如图所示,在Rt△ABC中,∠C=90°,点O在AB上,以O为圆心,OA长为半径的圆与AC,AB分别交于点D,E,且∠CBD=∠A,求证:BD与⊙O相切.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
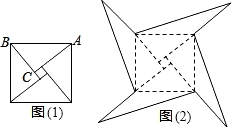 如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )
如图1是我国古代著名的“赵爽弦图”的示意图,它是由四个全等的直角三角形围成的.若AC=6,BC=5,将四个直角三角形中边长为6的直角边分别向外延长一倍,得到如图2所示的“数学风车”,则这个风车的外围周长是( )| A. | 36 | B. | 76 | C. | 66 | D. | 12 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
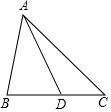 如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )
如图,△ABC中,点D在线段BC上,且△ABC∽△DBA,则下列结论一定正确的是( )| A. | AB2=BC•BD | B. | AB2=AC•BD | C. | AB•AD=BD•BC | D. | AB•AC=BC•BD |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,某轮船在海上以每小时30海里的速度向正西方向航行,上午8:00在点B处测得小岛A在北偏东30°方向,上午9:00船到达C处,测得岛A在北偏东45°方向,如果轮船继续向西航行,上午11:00到达点D处,求点D与小岛A的距离(精确到0.1海里)
如图,某轮船在海上以每小时30海里的速度向正西方向航行,上午8:00在点B处测得小岛A在北偏东30°方向,上午9:00船到达C处,测得岛A在北偏东45°方向,如果轮船继续向西航行,上午11:00到达点D处,求点D与小岛A的距离(精确到0.1海里)查看答案和解析>>
科目:初中数学 来源: 题型:解答题
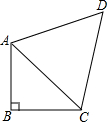 如图,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.
如图,∠ABC=90°,$\frac{AB}{AC}$=$\frac{\sqrt{7}}{4}$,BC=6,AD=DC,∠ADC=60°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com