
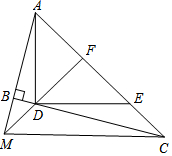
 如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.
如图,∠ABC=90°,D、E分别在BC、AC上,AD⊥DE,且AD=DE,点F是AE的中点,FD与AB相交于点M.分析 (1)只要证明△ADE是等腰直角三角形即可解决问题;
(2)结论:AD⊥MC.首先证明△DFC≌△AFM(AAS),推出CF=MF,再证明DE∥CM,由AD⊥DE,即可推出AD⊥CM.
解答 (1)证明: ∵AD⊥DE,AD=DE,
∵AD⊥DE,AD=DE,
∴△ADE是等腰直角三角形,
∵AF=EF,
∴DF⊥AE,
即MF⊥AC.
(2)解:结论:AD⊥MC.
理由:∵△ADE是等腰直角三角形,F是AE中点,
∴DF⊥AE,DF=AF=EF,
又∵∠ABC=90°,
∠DCF,∠AMF都与∠MAC互余,
∴∠DCF=∠AMF,
在△DFC和△AFM中,
$\left\{\begin{array}{l}{∠DCF=∠AMF}\\{∠CFD=∠MFA}\\{DF=AF}\end{array}\right.$,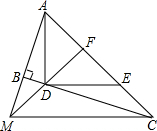
∴△DFC≌△AFM(AAS),
∴CF=MF,∵∠MFC=90°
∴∠FCM=∠AED=45°,
∴DE∥CM,∵⊥DE,
∴AD⊥CM.
点评 本题考查全等三角形的判定和性质、等腰直角三角形的性质等知识,解题的关键是灵活运用所学知识解决问题,属于中考常考题型.


 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
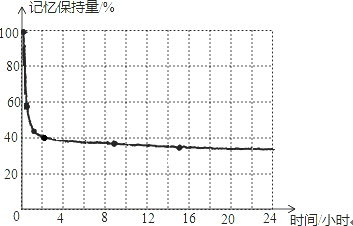 德国心理学家艾宾浩斯(H•Ebbinghaus)研究发现,遗忘在学习之后立即开始,遗忘是有规律的.他用无意义音节作记忆材料,用节省法计算保持和遗忘的数量.通过测试,他得到了一些数据,根据这些数据绘制出一条曲线,即著名的艾宾浩斯记忆遗忘曲线,如图.该曲线对人类记忆认知研究产生了重大影响.小梅观察曲线,得出以下四个结论:
德国心理学家艾宾浩斯(H•Ebbinghaus)研究发现,遗忘在学习之后立即开始,遗忘是有规律的.他用无意义音节作记忆材料,用节省法计算保持和遗忘的数量.通过测试,他得到了一些数据,根据这些数据绘制出一条曲线,即著名的艾宾浩斯记忆遗忘曲线,如图.该曲线对人类记忆认知研究产生了重大影响.小梅观察曲线,得出以下四个结论:| A. | ① | B. | ② | C. | ③ | D. | ④ |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com