
【题目】如图,一次函数y=ax+b的图象与反比例函数![]() 的图象交于A(﹣2,m),B
的图象交于A(﹣2,m),B
(4,﹣2)两点,与x轴交于C点,过A作AD⊥x轴于D.
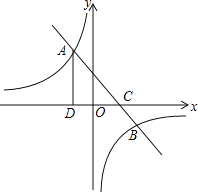
(1)求这两个函数的解析式:
(2)求△ADC的面积.
【答案】(1)![]() ;y=﹣x+2;(2)S△ADC=8
;y=﹣x+2;(2)S△ADC=8
【解析】
(1)因为反比例函数过A、B两点,所以可求其解析式和m的值,从而知A点坐标,进而求一次函数解析式.
(2)先求出直线AB与与x轴的交点C的坐标,再根据三角形的面积公式求解即可.
解:(1)∵反比例函数![]() 的图象过B(4,﹣2)点,∴k=4×(﹣2)=﹣8.
的图象过B(4,﹣2)点,∴k=4×(﹣2)=﹣8.
∴反比例函数的解析式为![]() .
.
∵反比例函数![]() 的图象过点A(﹣2,m),∴
的图象过点A(﹣2,m),∴![]() .∴A(﹣2,4).
.∴A(﹣2,4).
∵一次函数y=ax+b的图象过A(﹣2,4),B(4,﹣2)两点,
∴![]() ,解得
,解得![]() .
.
∴一次函数的解析式为y=﹣x+2;
(2)∵直线AB:y=﹣x+2交x轴于点C,∴C(2,0).
∵AD⊥x轴于D,A(﹣2,4),∴CD=2﹣(﹣2)=4,AD=4.
∴S△ADC=![]() CDAD=
CDAD=![]() ×4×4=8.
×4×4=8.


 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案科目:初中数学 来源: 题型:
【题目】某商场为了吸引顾客,设立了可以自由转动的转盘(如图,转盘被均匀分为20份),并规定:顾客每购买200元的商品,就能获得一次转动转盘的机会.如果转盘停止后,指针正好对准红色、黄色、绿色区域,那么顾客就可以分别获得200元、100元、50元的购物券,凭购物券可以在该商场继续购物.如果顾客不愿意转转盘,那么可以直接获得购物券30元.
(1)求转动一次转盘获得购物券的概率;
(2)转转盘和直接获得购物券,你认为哪种方式对顾客更合算?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一列从小到大,按某种规律排列的数如下:![]() ,3,7,□,15,19,23,□,31,35,□,…,第
,3,7,□,15,19,23,□,31,35,□,…,第![]() (
(![]() 为正整数)个数记作
为正整数)个数记作![]() ,
,![]() 是
是![]() 的函数,则
的函数,则![]() 的值可能是下列个数中的( ).
的值可能是下列个数中的( ).
A.158B.124C.79D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1(注:与图2完全相同),二次函数y= ![]() x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.
x2+bx+c的图象与x轴交于A(3,0),B(﹣1,0)两点,与y轴交于点C.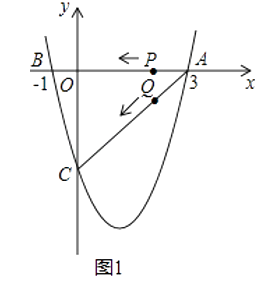
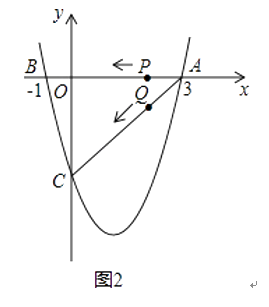
(1)求该二次函数的解析式;
(2)设该抛物线的顶点为D,求△ACD的面积(请在图1中探索);
(3)若点P,Q同时从A点出发,都以每秒1个单位长度的速度分别沿AB,AC边运动,其中一点到达端点时,另一点也随之停止运动,当P,Q运动到t秒时,△APQ沿PQ所在的直线翻折,点A恰好落在抛物线上E点处,请直接判定此时四边形APEQ的形状,并求出E点坐标(请在图2中探索).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是平行四边形,∠EAD=∠BAF

(1)试说明:△CEF为等腰三角形;
(2)猜测CE与CF的和与□ABCD的周长有何关系,并说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】完成下列推理论证过程:
如图,已知∠A=∠EDF,∠C=∠F,
求证:BC∥EF
证明:∵∠A=∠EDF( )
∴________∥________( )
∴∠C=∠BGD( )
又∵∠C=∠F ( 已知 )
∴_______=∠F(等量代换 )
∴BC∥EF( )
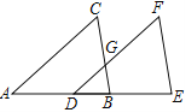
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知△ABC是等边三角形,点D,E分别在边BC,AC上,且CD=CE,连接DE并延长至点F,使EF=AE,连接AF,CF,连接BE并延长交CF于点G.下列结论:
①△ABE≌△ACF;②BC=DF;③S△ABC=S△ACF+S△DCF;④若BD=2DC,则GF=2EG.其中正确的结论是 . (填写所有正确结论的序号)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC的顶点坐标分别为A(﹣6,0),B(4,0),C(0,8),把△ABC沿直线BC翻折,点A的对应点为D,抛物线y=ax2﹣10ax+c经过点C,顶点M在直线BC上.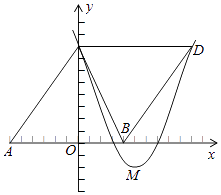
(1)证明四边形ABCD是菱形,并求点D的坐标;
(2)求抛物线的对称轴和函数表达式;
(3)在抛物线上是否存在点P,使得△PBD与△PCD的面积相等?若存在,直接写出点P的坐标;若不存在,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=﹣ ![]() x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
x2+bx+e与x轴交于点A(﹣3,0)、点B(9,0),与y轴交于点C,顶点为D,连接AD、DB,点P为线段AD上一动点.
(1)求抛物线的解析式;
(2)如图1,过点P作BD的平行线,交AB于点Q,连接DQ,设AQ=m,△PDQ的面积为S,求S关于m的函数解析式,以及S的最大值;
(3)如图2,抛物线对称轴与x轴交与点G,E为OG的中点,F为点C关于DG对称的对称点,过点P分别作直线EF、DG的垂线,垂足为M、N,连接MN,直接写出△PMN为等腰三角形时点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com