
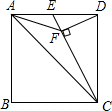
 如图,在正方形ABCD中,E是AD的中点,DF⊥EC于点F,连结AF,则下列四个结论:
如图,在正方形ABCD中,E是AD的中点,DF⊥EC于点F,连结AF,则下列四个结论:分析 ①正确,可以根据AA进行证明,②错误.先证明△AEF∽△CEA得∠EAF=∠ACE,通过计算发现AF≠FC即∠FAC≠∠FCA,由此可以作出判断.③正确.求出AF,即可解决问题.④正确,只要证明FC=4EF即可.
解答 解:设正方形ABCD边长为2a,则AE=ED=a,
∵四边形ABCD是正方形,
∴AB=BC=CD=AD=2a,∠ADC=90°,
∵DF⊥EC,
∴∠EDC=∠EFD=90°,
∵∠DEF=∠DEC,
∴△EDF∽△ECD,故①正确;
∴$\frac{ED}{EC}$=$\frac{DF}{CD}$=$\frac{EF}{ED}$,
∴$\frac{a}{\sqrt{5}a}$=$\frac{DF}{2a}$=$\frac{EF}{a}$,DE2=EF•EC,
∴EF=$\frac{\sqrt{5}}{5}$a,DF=$\frac{2\sqrt{5}}{5}$a,
FC=$\frac{4\sqrt{5}}{5}$a,
∴FC=4EF,
∴S△AFC=4S△AEF,故④正确;
∴AE2=EF•EC,
∴$\frac{AE}{EF}$=$\frac{EC}{AE}$,∵∠AEF=∠AEC,
∴△AEF∽△CEA,
∴$\frac{AF}{AC}$=$\frac{AE}{EC}$=$\frac{EF}{AE}$,∠EAF=∠ACE,
∴$\frac{AF}{2\sqrt{2}a}$=$\frac{a}{\sqrt{5}a}$,
∴AF=$\frac{2\sqrt{10}}{5}$a,
∴AF≠FC,
∴∠FAC≠∠FCA,
∴∠EAF≠∠FAC,故②错误;
∴AF:AB=$\frac{2\sqrt{10}}{5}a$:2a=$\sqrt{10}$:5=$\sqrt{2}$:$\sqrt{5}$,故③正确.
故答案为①③④.
点评 本题考查学相似三角形的判定和性质、正方形的性质勾股定理等知识,解题的关键是正确寻找相似三角形,利用相似三角形的性质解决问题,属于中考常考题型.


科目:初中数学 来源: 题型:填空题
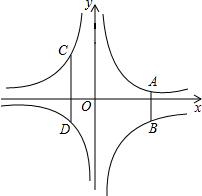 如图,已知点A,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥y轴,AB,CD在x轴的两侧,AB=1,CD=2,AB与CD的距离为3,则a-b的值是2.
如图,已知点A,D在反比例函数y=$\frac{a}{x}$(a>0)的图象上,点B,C在反比例函数y=$\frac{b}{x}$(b<0)的图象上,AB∥CD∥y轴,AB,CD在x轴的两侧,AB=1,CD=2,AB与CD的距离为3,则a-b的值是2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
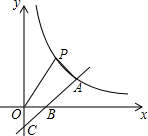 如图,一次函数y=x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,m),与x轴、y轴分别交于B、C两点,C点坐标为(0,-1).
如图,一次函数y=x+b与反比例函数y=$\frac{k}{x}$(x>0)的图象交于点A(2,m),与x轴、y轴分别交于B、C两点,C点坐标为(0,-1).查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
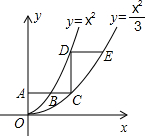 如图,平行于x轴的直线AC分别交抛物线${y_1}={x^2}$(x≥0)与${y_2}=\frac{x^2}{3}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E.若已知点A的纵坐标为1,则CD的长度为2,$\frac{DE}{AB}$=3-$\sqrt{3}$.
如图,平行于x轴的直线AC分别交抛物线${y_1}={x^2}$(x≥0)与${y_2}=\frac{x^2}{3}$(x≥0)于B、C两点,过点C作y轴的平行线交y1于点D,直线DE∥AC,交y2于点E.若已知点A的纵坐标为1,则CD的长度为2,$\frac{DE}{AB}$=3-$\sqrt{3}$.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com