

分析 (1)根据翻折变换的性质得出∠PBC=∠BPH,由平行线的性质得出∠APB=∠PBC,得出∠APB=∠BPH,即可得出结果;
(2)过B作BQ⊥PH,垂足为Q;首先证明△ABP≌△QBP,进而得出△BCH≌△BQH,即可得出PD+DH+PH=AP+PD+DH+HC=AD+CD=8.
解答 解:(1)∵PE=BE,
∴∠EBP=∠EPB,
又∵∠EPH=∠EBC=90°,
∴∠EPH-∠EPB=∠EBC-∠EBP,
即∠PBC=∠BPH,
又∵AD∥BC,
∴∠APB=∠PBC,
∴∠APB=∠BPH,
∵∠ABP=25°,
∴∠APB=65°
∴∠BPH=65°.
(2)△PHD的周长不变,为定值8.理由如下:
过B作BQ⊥PH,垂足为Q;如图所示: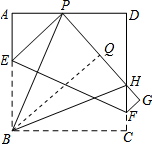
由(1)知∠APB=∠BPH,
在△ABP和△QBP中,
$\left\{\begin{array}{l}{∠APB=∠BPH}\\{∠A=∠BQP}\\{BP=BP}\end{array}\right.$,
∴△ABP≌△QBP(AAS).
∴AP=QP,AB=QB.
又∵AB=BC,
∴BC=BQ.
在Rt△BCH和Rt△BQH中,
$\left\{\begin{array}{l}{BH=BH}\\{BC=BQ}\end{array}\right.$,
∴Rt△BCH≌Rt△BQH(HL).
∴CH=QH.
∴△PHD的周长=PD+DH+PH=AP+PD+DH+HC=AD+CD=8.
点评 此题主要考查了翻折变换的性质、正方形的性质、全等三角形的判定与性质、直角三角形的性质;熟练掌握翻折变换和正方形的性质,并能进行推理论证与计算是解决问题的关键.


 同步学典一课多练系列答案
同步学典一课多练系列答案 经典密卷系列答案
经典密卷系列答案 金牌课堂练系列答案
金牌课堂练系列答案科目:初中数学 来源: 题型:解答题
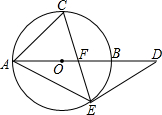 如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CE交AB于F,过E作⊙O的切线交AB的延长线于D.
如图,AB为⊙O的直径,点C为$\widehat{AB}$的中点,弦CE交AB于F,过E作⊙O的切线交AB的延长线于D.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
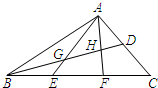 如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )
如图,在△ABC中,AD=DC,BE=EF=FC,AE、AF与BD相交于点G、H.已知${S_{△AHD}}=\frac{3}{10}$,则S四边形GEFH的值是( )| A. | $\frac{1}{2}$ | B. | $\frac{7}{10}$ | C. | $\frac{6}{11}$ | D. | $\frac{11}{20}$ |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com