Question

4．直线与四边形的关系我们给出如下定义：如图1，当一条直线与一个四边形没有公共点时，我们称这条直线和这个四边形相离．如图2，当一条直线与一个四边形有唯一公共点时，我们称这条直线和这个四边形相切．如图3，当一条直线与一个四边形有两个公共点时，我们称这条直线和这个四边形相交．
（1）如图4，矩形AOBC在平面直角坐标系xOy中，点A在x轴上，点B在y轴上，OA=3，OB=2，直线y=x+2与矩形AOBC的关系为相切．
（2）在（1）的条件下，直线y=x+2经过平移得到直线y=x+b，
当直线y=x+b，与矩形AOBC相离时，b的取值范围是b＜-3或b＞2  ；
当直线y=x+b，与矩形AOBC相交时，b的取值范围是-3＜b＜2 ．
（3）已知P（m，m+2），Q（3，m+2），M（3，1），N（m，1），当直线y=x+2与四边形PQMN相切且线段QN最小时，利用图5求直线QN的函数表达式．

Answer 1

分析 （1）由直线y=x+2过点B且BC平行x轴，结合直线与四边形的关系即可得出结论；
（2）依照题意画出图形．①根据图形求出相切时的b值，利用“比大的大，比小的小”即可得出结论；②根据相切时的b的值，取二者之间的数即是相交；
（3）根据矩形的性质（矩形的对角线相等）以及点到直线垂线段最短，确定点P、Q、N的位置，再通过角的计算可得出当QN最小时矩形PQMN是正方形，由正方形的邻边相等可求出m值，将其代入点Q、N的坐标中，利用待定系数法即可求出直线QN的函数表达式．

解答 解：（1）∵OB=2，
∴点B（0，2），
令y=x+2中x=0，则y=2，
∴直线y=x+2过点B，
又∵BC平行x轴，
∴直线y=x+2与矩形AOBC只有一个交点，
∴直线y=x+2与矩形AOBC相切．
故答案为：相切．
（2）依照题意画出图形，如图6所示．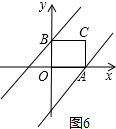
①当y=x+b过点B时，b=2；
当y=x+b过点A时，有0=3+b，解得：b=-3．
∴当直线y=x+b与矩形AOBC相离时，b＜-3或b＞2．
故答案为：b＜-3或b＞2．
②由①可知：当直线y=x+b与矩形AOBC相交时，-3＜b＜2．
故答案为：-3＜b＜2．
（3）∵P（m，m+2），Q（3，m+2），M（3，1），N（m，1），
∴PQ∥MN，PN∥QM，PN⊥x轴，
∴四边形PQMN是矩形，
∴PM=QN．
令y=x+2中x=3，则y=5，
∵5＞1，
∴点M在直线y=x+2的下方，
∵直线y=x+2与矩形PQMN相切，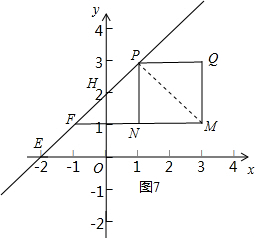
∴y=x+2必过P点．
∵线段QN最短，QN=PM，
∴只需线段PM最短即可．
根据点到直线的距离，垂线段最短，得MP垂直直线时最短，如图7所示．
∵y=x+2，
∴E（-2，0），H（0，2），
∴OE=OH，
∴∠OEH=45°．
∵FN∥x轴，
∴∠MFP=45°，
当∠NMP=45°时，∠MPF=90°，MP⊥EH，此时MP最短，
∵∠NMP=45°，∠PNM=90°，
∴∠NPM=45°，
∴PN=MN，
∴矩形PQMN是正方形时线段QN最短．
∵PN=m+1，MN=3-m，
∴m+1=3-m，
∴m=1，
∴Q（3，3），N（1，1）．
设直线QN的函数表达式为y=kx+c，
则有$\left\{\begin{array}{l}{3=3k+c}\\{1=k+c}\end{array}\right.$，解得：$\left\{\begin{array}{l}{k=1}\\{c=0}\end{array}\right.$，
∴直线QN的函数表达式为y=x．

点评 本题考查了待定系数法求函数解析式、矩形的性质以及正方形的判定与性质，解题的关键是：（1）由点B在直线上得出相切；（2）求出相切时的b值；（3）找出点Q、N的坐标．本题属于中档题，难度不大，解决该题型题目时，结合矩形与正方形的性质找出点的坐标，再利用待定系数法求出函数解析式是关键．