
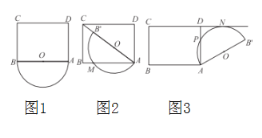
【题目】在矩形![]() 中,
中,![]() ,以
,以![]() 为直径的半圆
为直径的半圆![]() 在矩形
在矩形![]() 的外部,如图1,将半圆
的外部,如图1,将半圆![]() 绕点
绕点![]() 顺时针旋转α度(0°≤ɑ≤180°).
顺时针旋转α度(0°≤ɑ≤180°).
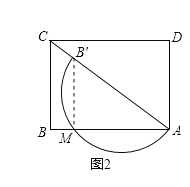
(1)在旋转过程中,![]() 的最小值是_____________,当半圆
的最小值是_____________,当半圆![]() 的直径落在对角线
的直径落在对角线![]() 上时,如图2,设半圆
上时,如图2,设半圆![]() 与
与![]() 的交点为
的交点为![]() ,则
,则![]() 长为__________.
长为__________.
(2)将半圆![]() 与直线
与直线![]() 相切时,切点为
相切时,切点为![]() ,半圆
,半圆![]() 与线段
与线段![]() 的交点为
的交点为![]() ,如图3,求劣弧
,如图3,求劣弧![]() 的长;
的长;
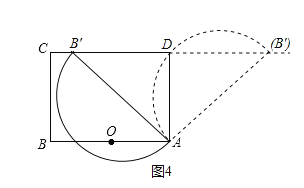
(3)在旋转过程中,当半圆弧与直线![]() 只有一个交点时,设此交点与点
只有一个交点时,设此交点与点![]() 的距离为
的距离为![]() 请直接写出
请直接写出![]() 的取值范围.
的取值范围.
【答案】(1)1;![]() ;(2)
;(2)![]() ;(3)
;(3)![]() 或
或![]()
【解析】
(1)连接B′M,则∠B′MA=90°,在Rt△ABC中,利用勾股定理可求出AC的长度,由∠B=∠B′MA=90°、∠BCA=∠MAB′可得出△ABC∽△AMB′,根据相似三角形的性质可求出AM的长度;
(2)连接OP、ON,过点O作OG⊥AD于点G,则四边形DGON为矩形,进而可得出DG、AG的长度,在Rt△AGO中,由AO=2、AG=1可得出∠OAG=60°,进而可得出△AOP为等边三角形,再利用弧长公式即可求出劣弧AP的长;
(3)由(2)可知:△AOP为等边三角形,根据等边三角形的性质可求出OG、DN的长度,进而可得出CN的长度,画出点B′在直线CD上的图形,在Rt△AB′D中(点B′在点D左边),利用勾股定理可求出B′D的长度进而可得出CB′的长度,再结合图形即可得出:半圆弧与直线CD只有一个交点时d的取值范围.
解:(1)∵在矩形ABCD中,AB=4,BC=3,
∴AC=5,
在旋转过程中,当点B′落在对角线AC上时,B′C的值最小,最小值为1;
在图2中,连接B′M,则∠B′MA=90°,
在Rt△ABC中,AB=4,BC=3,
∴AC=5,
∵∠B=∠B′MA=90°,∠BCA=∠MAB′,
∴△ABC∽△AMB′,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
故答案为:1,![]() ;
;
(2)解:如图3,连接![]() ,过
,过![]() 作
作![]() 于点
于点![]() ,
,
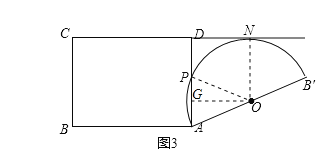
∵半圆![]() 与直线
与直线![]() 相切,
相切,
![]() ,
,
∴四边形![]() 为矩形,
为矩形,
∴![]() ,
,
在![]() 中,
中,![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,
![]() 为等边三角形,
为等边三角形,
![]() ,
,
∴劣弧![]() 的长=
的长=![]() ;
;
(3)由(2)可知:△AOP为等边三角形,
∴![]() ,
,
∴![]() ,
,
当点B′在直线CD上时,如图4所示,
在Rt△AB′D中(点B′在点D左边),AB′=4,AD=3,
∴![]() ,
,
∴![]() ,
,
∵AB′为直径,
∴∠AD B′=90°,
∴当点B′在点D右边时,半圆交直线CD于点D、B′,
∴当半圆弧与直线CD只有一个交点时,![]() 或
或![]() .
.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列结论:①abc>0;②2a+b=0;③若m为任意实数,则a+b>am2+bm;④a﹣b+c>0;⑤若ax12+bx1=ax22+bx2,且x1≠x2,则x1+x2=2.其中,正确结论的个数为( )
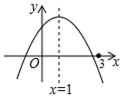
A.1B.2C.3D.4
查看答案和解析>>
科目:初中数学 来源: 题型:
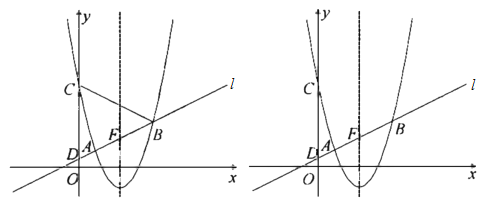
【题目】如图,在平面直角坐标系![]() 中,以直线
中,以直线![]() 为对称轴的抛物线
为对称轴的抛物线![]() 与直线
与直线![]() 交于
交于![]() ,
,![]() 两点,与
两点,与![]() 轴交于
轴交于![]() ,直线
,直线![]() 与
与![]() 轴交于点
轴交于点![]() .
.
(1)求抛物线的函数表达式;
(2)设直线![]() 与抛物线的对称轴的交点为
与抛物线的对称轴的交点为![]() ,
,![]() 是抛物线上位于对称轴右侧的一点,若
是抛物线上位于对称轴右侧的一点,若![]() ,且
,且![]() 与
与![]() 的面积相等,求点
的面积相等,求点![]() 的坐标;
的坐标;
(3)若在![]() 轴上有且只有一点
轴上有且只有一点![]() ,使
,使![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等边三角形![]() 边长是定值,点
边长是定值,点![]() 是它的外心,过点
是它的外心,过点![]() 任意作一条直线分别交
任意作一条直线分别交![]() 于点
于点![]() ,将
,将![]() 沿直线
沿直线![]() 折叠,得到
折叠,得到![]() ,若
,若![]() 分别交
分别交![]() 于点
于点![]() ,连接
,连接![]() ,则下列判断错误的是( )
,则下列判断错误的是( )
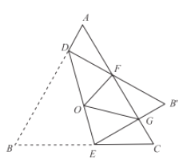
A.△![]() ≌△
≌△![]()
B.![]() 的周长是一个定值
的周长是一个定值
C.四边形![]() 的面积是一个定值
的面积是一个定值
D.四边形![]() 的面积是一个定值
的面积是一个定值
查看答案和解析>>
科目:初中数学 来源: 题型:
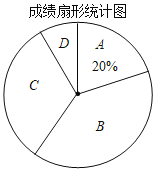
【题目】在第二届数字中国建设峰会召开之际,某校举行了第二届“掌握新技术,走进数时代”信息技术应用大赛,将该校八年级参加竞赛的学生成绩统计后,绘制成如下统计图表(不完整):
成绩频数分布统计表
组别 | A | B | C | D |
成绩x(分) | 60≤x<70 | 70≤x<80 | 80≤x<90 | 90≤x<100 |
人数 | 10 | m | 16 | 4 |
请观察上面的图表,解答下列问题:
(1)统计表中m= ,D组的圆心角为 °;
(2)D组的4名学生中,有2名男生和2名女生.从D组随机抽取2名学生参加5G体验活动,请你画出树状图或用列表法求:
①恰好1名男生和1名女生被抽取参加5G体验活动的概率;
②至少1名女生被抽取参加5G体验活动的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,抛物线y=﹣![]() x2+bx+c与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D,B(﹣3,0),A(0,
x2+bx+c与x轴交于B、C两点(点B在点C的左侧),与y轴交于点A,抛物线的顶点为D,B(﹣3,0),A(0,![]() )
)
(1)求抛物线解析式及D点坐标;
(2)如图1,P为线段OB上(不与O、B重舍)一动点,过点P作y轴的平行线交线段AB于点M,交抛物线于点N,点N作NK⊥BA交BA于点K,当△MNK与△MPB的面积相等时,在X轴上找一动点Q,使得![]() CQ+QN最小时,求点Q的坐标及
CQ+QN最小时,求点Q的坐标及![]() CQ+QN最小值;
CQ+QN最小值;
(3)如图2,在(2)的条件下,将△ODN沿射线DN平移,平移后的对应三角形为△O′D′N′,将△AOC绕点O逆时针旋转到A1OC1的位置,且点C1恰好落在AC上,△A1D′N′是否能为等腰三角形,若能求出N′的坐标,若不能,请说明理由.
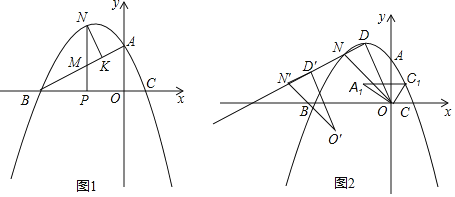
查看答案和解析>>
科目:初中数学 来源: 题型:
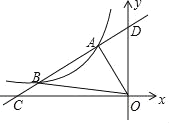
【题目】如图,直线y=kx+b与反比例函数![]() 的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C,D.
的图象分别交于点A(﹣1,2),点B(﹣4,n),与x轴,y轴分别交于点C,D.
(1)求此一次函数和反比例函数的解析式;
(2)求△AOB的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com