
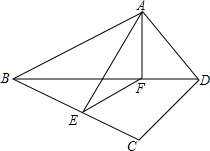
 已知:四边形ABCD中,AD=CD,对角线BD平分∠ADC,点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接EF,AF,AE.
已知:四边形ABCD中,AD=CD,对角线BD平分∠ADC,点E,F分别是线段BC和线段BD上的点,且点F在线段EC的垂直平分线上,连接EF,AF,AE.分析 (1)由△ADF≌△CDF得AF=CF,又点F在线段EC的垂直平分线上得EF=C即可证明.
(2)先证明∠FEC=∠BAF得A、B、E、F四点共圆故∠EAF=∠EBH=∠ABD.
解答 (1)证明:如图,连接CF.
∵BD平分∠ADC,
∴∠ADB=∠CDB,
在△ADF和△CDF中,
$\left\{\begin{array}{l}{AD=DC}\\{∠ADF=∠CDF}\\{DF=DF}\end{array}\right.$,
∴△ADF≌△CDF,
∴AF=CF,
∵点F在线段EC的垂直平分线上,
∴EF=CF,
∴AF=EF.
(2)证明:∵BD平分∠ADC,
∴∠ADB=∠CDB
在△ADB和△CDB中,
$\left\{\begin{array}{l}{AD=CD}\\{∠ADB=∠CDB}\\{BD=BD}\end{array}\right.$,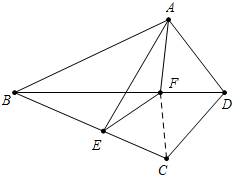
∴△ADB≌△CDB,
∴∠ABD=∠CBD,AB=BC,
在△BAF和△BCF中,
$\left\{\begin{array}{l}{AB=BC}\\{∠ABF=∠CBF}\\{BF=BF}\end{array}\right.$,
∴△BFA≌△BFC,
∴∠BAF=∠BCF,
∵FE=FC,
∴∠FEC=∠FCE,
∴∠FEC=∠BAF,
∴A、B、E、F四点共圆,
∴∠EAF=∠EBH=∠ABD.
点评 本题考查全等三角形的判定和性质、垂直平分线的性质、四点共圆等知识,充分利用三角形全等是解决问题的关键.


 鸿图图书寒假作业假期作业吉林大学出版社系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案科目:初中数学 来源: 题型:解答题
| 序号 | 1 | 2 | 3 | 4 | 5 | 6 |
| 笔试成绩 | 66 | 90 | 86 | 64 | 65 | 84 |
| 专业技能测试成绩 | 95 | 92 | 93 | 80 | 88 | 92 |
| 说课成绩 | 85 | 78 | 86 | 88 | 94 | 85 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是2$\sqrt{5}$-2.
如图,点P是正方形ABCD的对角线BD上的一个动点(不与B、D重合),连结AP,过点B作直线AP的垂线,垂足为H,连结DH.若正方形的边长为4,则线段DH长度的最小值是2$\sqrt{5}$-2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,∠AOB=90°,将三角尺的直角顶点落在∠AOB的角平分线OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F,求证:PE=PF.
如图,∠AOB=90°,将三角尺的直角顶点落在∠AOB的角平分线OC的任意一点P上,使三角尺的两条直角边与∠AOB的两边分别相交于点E、F,求证:PE=PF.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 已知数轴上A、B两点对应数分别为-2和4,P为数轴上一动点,对应数为x.
已知数轴上A、B两点对应数分别为-2和4,P为数轴上一动点,对应数为x.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com