
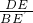 ,另外,对kB、kC作类似的规定.
,另外,对kB、kC作类似的规定.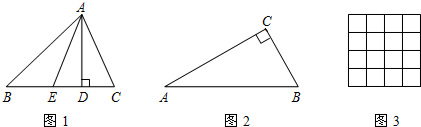
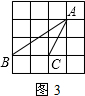
 解:(1)在△ABC中,∠C=90°,∠A=30°时,BC边上的高,垂足就是点C,设中线是AD,则kA=
解:(1)在△ABC中,∠C=90°,∠A=30°时,BC边上的高,垂足就是点C,设中线是AD,则kA= =1;
=1; AB=BF,
AB=BF, BF=
BF= AF,
AF, =
= ;
; ;
; ,而△ABC是直角三角形,故命题错误;
,而△ABC是直角三角形,故命题错误;

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:解答题
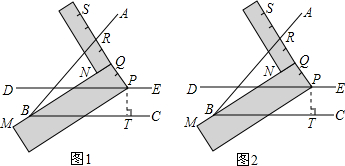 (1)阅读理解:
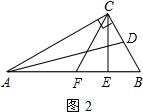
(1)阅读理解: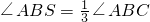 是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出
是否成立?如果成立,请说明理由;如果不成立,请在图2中∠ABC的外部画出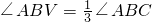 (无需写画法,保留画图痕迹即可).
(无需写画法,保留画图痕迹即可).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com