
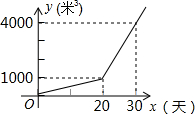
 某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图所示,当总用水量为2500米3时,该经济作物种植时间是25天.
某农户种植一种经济作物,总用水量y(米3)与种植时间x(天)之间的函数关系如图所示,当总用水量为2500米3时,该经济作物种植时间是25天. 分析 由图可知x>20时,函数关系式为一次函数关系式,把(20,1000),(30,4000)代入可得相关函数关系式;若达到2500米3,代入y可得相应的天数.
解答 解:当x>20时,设y=ax+b.
∵x=20时,y=1000,x=30时,y=4000.
∴$\left\{\begin{array}{l}{20a+b=1000}\\{30a+b=4000}\end{array}\right.$,
解得$\left\{\begin{array}{l}{a=300}\\{b=-5000}\end{array}\right.$.
∴y=300x-5000.
∴令y=2500,得300x-5000=2500,
x=25.
∴种植时间为25天时,总用水量达到2500米3.
故答案为:25.
点评 考查一次函数的应用;用待定系数法求函数关系式是常用的求函数关系式的方法.


科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE、AC、DE这三条线段之间有怎样的数量关系?请说明理由.
如图,在△ABC中,∠ACB=90°,BE平分∠ABC,DE⊥AB于D,如果AC=3cm,那么AE、AC、DE这三条线段之间有怎样的数量关系?请说明理由.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )
如图,D、E分别是△ABC的边AB、BC上的点,且DE∥AC,AE、CD相交于点O,若S△DOE:S△COA=1:25,则S△BDE与S△CDE的比是( )| A. | 1:3 | B. | 1:4 | C. | 1:5 | D. | 1:25 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
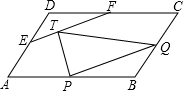 如图,在?ABCD中,分别设P,Q,E,F为边AB,BC,AD,CD的中点,设T为线段EF的三等分点,则△PQT与?ABCD的面积之比是1:4.
如图,在?ABCD中,分别设P,Q,E,F为边AB,BC,AD,CD的中点,设T为线段EF的三等分点,则△PQT与?ABCD的面积之比是1:4.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com