
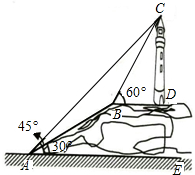
 如图,某教学学习小组为了测量山顶上一古灯塔的高度CD,他们在山脚下的点A处测得塔顶C处的仰角为45°,沿着坡角为30°的登山梯AB向上走200米到达山顶B处后,测得塔顶C处的仰角为60°,已知点B与底部D在同一水平线上.
如图,某教学学习小组为了测量山顶上一古灯塔的高度CD,他们在山脚下的点A处测得塔顶C处的仰角为45°,沿着坡角为30°的登山梯AB向上走200米到达山顶B处后,测得塔顶C处的仰角为60°,已知点B与底部D在同一水平线上.| 3 |
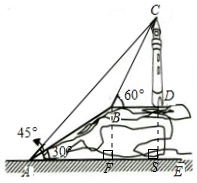 解:(1)作BF⊥AE,垂足为F;DS⊥AE,垂足为S.
解:(1)作BF⊥AE,垂足为F;DS⊥AE,垂足为S.| 3 |
| x |
| BD |
| ||
| 3 |
| ||
| 3 |
| 3 |
| ||
| 3 |
| 3 |


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
 三条直线AB,CD,EF,如果AB∥EF,CD∥EF,想一想直线AB与CD可能相交吗?为什么?
三条直线AB,CD,EF,如果AB∥EF,CD∥EF,想一想直线AB与CD可能相交吗?为什么?查看答案和解析>>
科目:初中数学 来源: 题型:
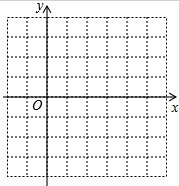 (1)请在网格坐标系中画出二次函数y=-x2+2x的大致图象.(注:图中小正方形网格的边长为1.)
(1)请在网格坐标系中画出二次函数y=-x2+2x的大致图象.(注:图中小正方形网格的边长为1.)查看答案和解析>>
科目:初中数学 来源: 题型:
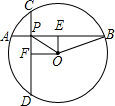 如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为P,OE⊥AB于E,OF⊥CD于F,
如图,在⊙O中,弦AB=CD,AB⊥CD,垂足为P,OE⊥AB于E,OF⊥CD于F,| 2 |
查看答案和解析>>
科目:初中数学 来源: 题型:
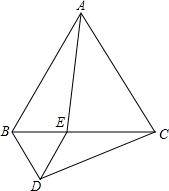 如图,等边三角形ABC的边长为2,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.
如图,等边三角形ABC的边长为2,点E是边BC上一动点(不与点B、C重合),以BE为边在BC的下方作等边三角形BDE,连接AE、CD.查看答案和解析>>
科目:初中数学 来源: 题型:
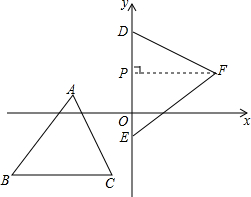 如图,在平面直角坐标系xOy中,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC.若A点的坐标为(-3,1),B、C两点的纵坐标均为-3,D、E两点在y轴上.
如图,在平面直角坐标系xOy中,△ABC与△DEF全等,其中A、B、C的对应顶点分别为D、E、F,且AB=BC.若A点的坐标为(-3,1),B、C两点的纵坐标均为-3,D、E两点在y轴上.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com