
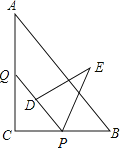
【题目】如图,Rt△ABC中,∠C=90°,AB=15,BC=9,点P,Q分别在BC,AC上,CP=3x,CQ=4x(0<x<3).把△PCQ绕点P旋转,得到△PDE,点D落在线段PQ上.
(1)求证:PQ∥AB;
(2)若点D在∠BAC的平分线上,求CP的长;
(3)若△PDE与△ABC重叠部分图形的周长为T,且12≤T≤16,求x的取值范围.
【答案】(1)证明见解析;(2)6;(3)1≤x≤![]() .
.
【解析】
(1)先根据勾股定理求出AC的长,再根据计算可知![]() ,结合定理两边成比例且夹角相等的三角形相似证明△PQC∽△BAC,再根据相似三角形的性质得出∠CPQ=∠B,由此可得出PQ∥AB;
,结合定理两边成比例且夹角相等的三角形相似证明△PQC∽△BAC,再根据相似三角形的性质得出∠CPQ=∠B,由此可得出PQ∥AB;
(2)连接AD,根据PQ∥AB和点D在∠BAC的平分线上可证∠ADQ=∠DAQ,由此可得AQ=DQ,分别表示AQ和DQ由此可得方程12﹣4x=2x,解出x,即可求出CP;·
(3)先求出当点E在AB上时x的值,再分![]() 两种情况进行分类讨论.
两种情况进行分类讨论.
(1)证明:∵在Rt△ABC中,AB=15,BC=9,
∴AC=![]() =
=![]() =12.
=12.
∵![]() =
=![]() =
=![]() ,
,![]() =
=![]() =
=![]() ,
,
∴![]() =
=![]() .
.
∵∠C=∠C,
∴△PQC∽△BAC,
∴∠CPQ=∠B,
∴PQ∥AB;
(2)解:连接AD,
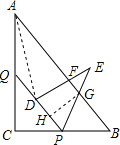
∵PQ∥AB,
∴∠ADQ=∠DAB.
∵点D在∠BAC的平分线上,
∴∠DAQ=∠DAB,
∴∠ADQ=∠DAQ,
∴AQ=DQ.
∵PD=PC=3x,QC=4x
∴在Rt△CPQ中,根据勾股定理PQ=5x.
∴DQ=2x.
∵AQ=12﹣4x,
∴12﹣4x=2x,解得x=2,
∴CP=3x=6.
(3)解:当点E在AB上时,
∵PQ∥AB,
∴∠DPE=∠PGB.
∵∠CPQ=∠DPE,∠CPQ=∠B,
∴∠B=∠PGB,
∴PB=PG=5x,
∴3x+5x=9,解得x=![]() .
.
①当0<x≤![]() 时,T=PD+DE+PE=3x+4x+5x=12x,此时0<T≤
时,T=PD+DE+PE=3x+4x+5x=12x,此时0<T≤![]() ;
;
②当![]() <x<3时,设PE交AB于点G,DE交AB于F,作GH⊥PQ,垂足为H,
<x<3时,设PE交AB于点G,DE交AB于F,作GH⊥PQ,垂足为H,
∴HG=DF,FG=DH,Rt△PHG∽Rt△PDE,
∴![]() =
=![]() =
=![]() .
.
∵PG=PB=9﹣3x,
∴![]() =
=![]() =
=![]() ,
,
∴GH=![]() (9﹣3x),PH=
(9﹣3x),PH=![]() (9﹣3x),
(9﹣3x),
∴FG=DH=3x﹣![]() (9﹣3x),
(9﹣3x),
∴T=PG+PD+DF+FG=(9﹣3x)+3x+![]() (9﹣3x)+[3x﹣
(9﹣3x)+[3x﹣![]() (9﹣3x)]
(9﹣3x)]
=![]() x+
x+![]() ,
,
此时,![]() <T<18.
<T<18.
∴当0<x<3时,T随x的增大而增大,
∴T=12时,即12x=12,解得x=1;
T=16时,即![]() x+
x+![]() =16,解得x=
=16,解得x=![]() .
.
∵12≤T≤16,
∴x的取值范围是1≤x≤![]() .
.


科目:初中数学 来源: 题型:
【题目】如图,已知A(﹣4,n),B(2,﹣4)是一次函数y=kx+b的图象和反比例函数y=![]() 的图象的两个交点.
的图象的两个交点.
(1)求反比例函数和一次函数的解析式;
(2)求直线AB与x轴的交点C的坐标及△AOB的面积;
(3)直接写出一次函数的值小于反比例函数值的x的取值范围.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列关于二次函数的说法错误的是( )
A.二次函数y=(x+2)2-2的顶点坐标是(-2,-2)
B.抛物线y=-x2 +2x+1,当x<0时y随x的增大而增大
C.函数y= 2x2 + 4x-3的图象的最低点坐标为(-1,-5)
D.点A(3,0)不在抛物线y=x2-2x-3的图象上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+3.
(1)求它的对称轴和顶点坐标;
(2)求该抛物线与x轴的交点坐标;
(3)建立平面直角坐标系,画出这条抛物线的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=﹣x2+2x+3.
(1)求它的对称轴和顶点坐标;
(2)求该抛物线与x轴的交点坐标;
(3)建立平面直角坐标系,画出这条抛物线的图象.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.袋中有形状、大小、质地完全一样的5个红球和1个白球,从中随机抽出一个球,一定是红球
B.天气预报“明天降水概率10%”,是指明天有10%的时间会下雨
C.某地发行一种福利彩票,中奖率是千分之一,那么,买这种彩票1000张,一定会中奖
D.连续掷一枚均匀硬币,若5次都是正面朝上,则第六次仍然可能正面朝上
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将△ABC绕点A顺时针旋转60°得到△ADE,点C的对应点E恰好落在BA的延长线上,DE与BC交于点F,连接BD.下列结论不一定正确的是( )
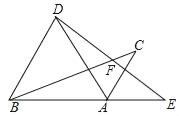
A. AD=BD B. AC∥BD C. DF=EF D. ∠CBD=∠E
查看答案和解析>>
科目:初中数学 来源: 题型:
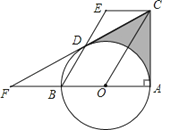
【题目】如图,AB是⊙O的直径,∠BAC=90°,四边形EBOC是平行四边形,EB交⊙O于点D,连接CD并延长交AB的延长线于点F.
(1)求证:CF是⊙O的切线;
(2)若∠F=30°,EB=4,求图中阴影部分的面积(结果保留根号和π)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某文具店购进一批纪念册,每本进价为20元,出于营销考虑,要求每本纪念册的售价不低于20元且不高于28元,在销售过程中发现该纪念册每周的销售量y(本)与每本纪念册的售价x(元)之间满足一次函数关系:当销售单价为22元时,销售量为36本;当销售单价为24元时,销售量为32本.
(1)求出y与x的函数关系式;
(2)当文具店每周销售这种纪念册获得150元的利润时,每本纪念册的销售单价是多少元?
(3)设该文具店每周销售这种纪念册所获得的利润为w元,将该纪念册销售单价定为多少元时,才能使文具店销售该纪念册所获利润最大?最大利润是多少?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com