
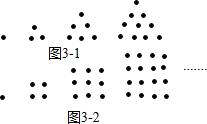
 古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:
古希腊人常用小石子在沙滩上摆成各种形状来研究数,例如:分析 (1)图1中1、3、6、10,…,第n个图中点的个数是1+2+3+…+n,即$\frac{n(n+1)}{2}$;图2中1、4、9、16,…,第n个图中点的个数是n2,求出能同时满足两个式子的数,即可得出结果;
(2)由(1)中规律可得$\frac{n(n+1)}{2}$=400,判断该方程有正无整数解即可;
(3)利用(1)中规律,分别列出方程求解可得.
解答 解:(1)∵正方形数点的个数是为n2,∴除1外,分别为4,9,16,25,36,49,64,…,
∵图1中1、3、6、10,…,第n个图中点的个数是1+2+3+…+n,即三角形数点的个数是为$\frac{n(n+1)}{2}$,
∵4=$\frac{n(n+1)}{2}$无正整数解,∴4不是三角形数,
∵9=$\frac{n(n+1)}{2}$无正整数解,∴9不是三角形数,
∵16=$\frac{n(n+1)}{2}$无正整数解,∴16不是三角形数,
∵25=$\frac{n(n+1)}{2}$无正整数解,∴25不是三角形数,
∵36=$\frac{n(n+1)}{2}$,解得n=8,所以36是三角形数,
∴除1外,最小的既是三角形数又是正方形数的是36,
故答案为:36
故答案为36;
(2)不是,
根据题意,$\frac{n(n+1)}{2}$=400,
∵方程无整数解,
∴400不是三角形数.
(3)1225既是正方形数又是三角形数,
由n2=1225可得n=35,
∴1225是第35个正方形数;
由$\frac{n(n+1)}{2}$=1225可得n=-50(舍)或n=49,
∴1225还是第49个三角形数.
点评 本题考查三角形数、正方形数的规律、完全平方数与归纳推理及一元二次方程等知识,观察已知式子的规律并改写形式是解决问题的关键.


科目:初中数学 来源: 题型:解答题
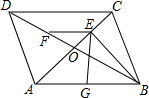 如图所示,在?ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点.证明:
如图所示,在?ABCD中,对角线AC、BD相交于点O,BD=2AD,E、F、G分别是OC、OD、AB的中点.证明:查看答案和解析>>
科目:初中数学 来源: 题型:选择题
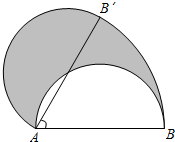 如图,直径AB为3的半圆,绕A点逆时针旋转60°,此时点B到了点B′处,则图中阴影部分的面积是( )
如图,直径AB为3的半圆,绕A点逆时针旋转60°,此时点B到了点B′处,则图中阴影部分的面积是( )| A. | 3π | B. | $\frac{3π}{2}$ | C. | 6π | D. | 24π |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 必然发生的事件发生的概率为1 | |
| B. | 不可能发生的事件发生的概率为0 | |
| C. | 不确定事件发生的概率为0 | |
| D. | 随机事件发生的概率介于0 和1之间 |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com