
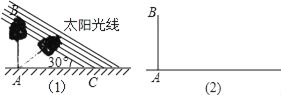
【题目】某数学兴趣小组,利用树影测量树高,如图(1),已测出树AB的影长AC为12米,并测出此时太阳光线与地面成30°夹角.
(1)求出树高AB;
(2)因水土流失,此时树AB沿太阳光线方向倒下,在倾倒过程中,树影长度发生了变化,假设太阳光线与地面夹角保持不变.求树的最大影长.(用图(2)解答)
【答案】(1)树AB的高约为4![]() m;(2)8
m;(2)8![]() m.
m.
【解析】
(1)AB=ACtan30°=12×![]() =
=![]() (米).
(米).
答:树高约为![]() 米.
米.
(2)如图(2),B1N=AN=AB1sin45°=![]() ×
×![]() =
=![]() (米).
(米).
NC1=NB1tan60°=![]() ×
×![]() =
=![]() (米).
(米).
AC1=AN+NC1=![]() +
+![]() .
.
当树与地面成60°角时影长最大AC2(或树与光线垂直时影长最大或光线与半径为AB的⊙A相切时影长最大)
AC2=2AB2=![]() ;
;
(1)在直角△ABC中,已知∠ACB=30°,AC=12米.利用三角函数即可求得AB的长;
(2)在△AB1C1中,已知AB1的长,即AB的长,∠B1AC1=45°,∠B1C1A=30°.过B1作AC1的垂线,在直角△AB1N中根据三角函数求得AN,BN;再在直角△B1NC1中,根据三角函数求得NC1的长,再根据当树与地面成60°角时影长最大,根据三角函数即可求解.


 尖子生新课堂课时作业系列答案
尖子生新课堂课时作业系列答案 英才计划同步课时高效训练系列答案
英才计划同步课时高效训练系列答案科目:初中数学 来源: 题型:
【题目】甲、乙两车分别从![]() 、
、![]() 两地同时相向匀速行驶,当乙车到达
两地同时相向匀速行驶,当乙车到达![]() 地后,继续保持原速向远离
地后,继续保持原速向远离![]() 的方向行驶,而甲车到达
的方向行驶,而甲车到达![]() 地后,休息半小时后立即掉头,并以原速的
地后,休息半小时后立即掉头,并以原速的![]() 倍与乙车同向行驶,经过一段时间后,两车先后到达距
倍与乙车同向行驶,经过一段时间后,两车先后到达距![]() 地
地![]() 的
的![]() 地并停下来,设两车行驶的时间为
地并停下来,设两车行驶的时间为![]() ,两车之间的距离为
,两车之间的距离为![]() ,
,![]() 与
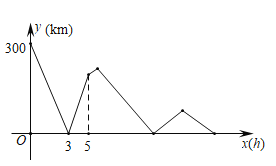
与![]() 的函数关系如图,则当甲车从
的函数关系如图,则当甲车从![]() 地掉头追到乙车时,乙车距离
地掉头追到乙车时,乙车距离![]() 地__________
地__________![]() .
.
查看答案和解析>>
科目:初中数学 来源: 题型:
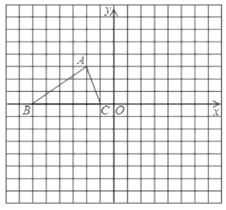
【题目】如图,已知![]() 的三个顶点的坐标分别为
的三个顶点的坐标分别为![]() 、
、![]() 、
、![]() .
.
(1)画出![]() 关于原点对称的三角形
关于原点对称的三角形![]() ;
;
(2)将三角形![]() 、
、![]() 、
、![]() 绕坐标原点
绕坐标原点![]() 逆时针旋转
逆时针旋转![]() ,画出图形,直接写出
,画出图形,直接写出![]() 的对应点的坐标.
的对应点的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,OA,OB是⊙O的两条半径,OA⊥OB,C是半径OB上一动点,连结AC并延长交⊙O于D,过点D作圆的切线交OB的延长线于E,已知OA=8.
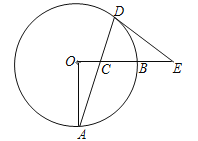
(1)求证:∠ECD=∠EDC;
(2)若tanA=![]() ,求DE长;
,求DE长;
(3)当∠A从15°增大到30°的过程中,求弦AD在圆内扫过的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个不透明的口袋里装有红、黑、绿三种颜色的乒乓球(除颜色外其余都相同),其中红球有![]() 个,黑球有
个,黑球有![]() 个,绿球有
个,绿球有![]() 个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为( )
个,第一次任意摸出一个球(不放回),第二次再摸出一个球,则两次摸到的都是红球的概率为( )
A. ![]() B.
B. ![]() C.
C. ![]() D.
D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】田忌赛马是一个为人熟知的故事.传说战国时期,齐王与田忌各有上、中、下三匹马,同等级的马中,齐王的马比田忌的马强.有一天,齐王要与田忌赛马,双方约定:比赛三局,每局各出-匹,每匹马赛一次,赢得两局者为胜.看样子田忌似乎没有什么胜的希望,但是田忌的谋士了解到主人的上、中等马分别比齐王的中、下等马要强.
(1)如果齐王将马按下中上的顺序出阵比赛,那么田忌的马如何出阵才能获胜?
(2)如果齐王将马按下中上的顺序出阵,而田忌的马随机出阵比赛,田忌获胜的概率是多少?(要求写出双方对阵的所有情况)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】汽车油箱中的余油量![]() (升)随汽车行驶的时间
(升)随汽车行驶的时间![]() (时)的变化而变化,
(时)的变化而变化,![]() 与
与![]() 之间的关系为
之间的关系为![]() ,其中
,其中![]() 是油箱中原有的油的升数,若这辆汽车油箱中原有油60升.
是油箱中原有的油的升数,若这辆汽车油箱中原有油60升.
(1)用表格表示行驶1到5小时过程中这辆汽车油箱中余油量与行驶时间![]() 的关系,填写下表:
的关系,填写下表:
行驶时间(时) | 1 | 2 | 3 | 4 | 5 |
余油量(升) |
(2)这辆车最多可行驶多少小时?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com