
【题目】在△ABC中,∠B=60°,D、E分别为AB、BC上的点,且AE、CD交于点F.
(1)如图1,若AE、CD为△ABC的角平分线:
①求∠AFD的度数;
②若AD=3,CE=2,求AC的长;
(2)如图2,若∠EAC=∠DCA=30°,求证:AD=CE.
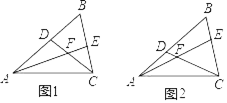
【答案】(1)①60°;②5;(2)详见解析.
【解析】
(1)①根据角平分线的定义、三角形内角和定理计算;
②在AC上截取AG=AD=3,连接FG,证明△ADF≌△AGF、△CGF≌△CEF,根据全等三角形的性质解答;
(2)在AE上截取FH=FD,连接CH,证明△ADF≌△CHF,根据全等三角形的性质、三角形的外角的性质解答.
解:(1)①∵AE、CD分别为△ABC的角平分线,
∴∠FAC=![]() ∠BAC,∠FCA=
∠BAC,∠FCA=![]() ∠BCA,
∠BCA,
∵∠B=60°
∴∠BAC+∠BCA=120°,
∴∠AFC=180﹣∠FAC﹣∠FCA=180﹣![]() (∠BAC+∠BCA)=120°
(∠BAC+∠BCA)=120°
∴∠AFD=180°-∠AFC=60°;
②在AC上截取AG=AD=3,连接FG,
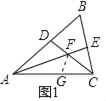
∵AE、CD分别为△ABC的角平分线,
∴∠FAC=∠FAD,∠FCA=∠FCE,
∵∠AFC=120°,
∴∠AFD=∠CFE=60°,
在△ADF和△AGF中,
∵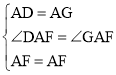 ,
,
∴△ADF≌△AGF(SAS),
∴∠AFD=∠AFG=60°,
∴∠GFC=∠CFE=60°,
在△CGF和△CEF中,
∵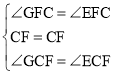 ,
,
∴△CGF≌△CEF(ASA),
∴CG=CE=2,
∴AC=5;
(2)在AE上截取FH=FD,连接CH,
∵∠FAC=∠FCA=30°,
∴FA=FC,
在△ADF和△CHF中,
∵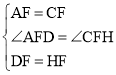 ,
,
∴△ADF≌△CHF(SAS),
∴AD=CH,∠DAF=∠HCF,
∵∠CEH=∠B+∠DAF=60°+∠DAF,
∠CHE=∠HAC+∠HCA=60°+∠HCF,
∴∠CEH=∠CHE,
∴CH=CE,
∴AD=CE.


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】如图:已知在平面直角坐标系中,△ABC的位置如图所示:
(1)请写出点A、B、C三点的坐标.
(2)将△ABC向右平移6个单位,再向上平移2个单位,请在图中作出平移后的△A'B'C',并写出它们的坐标:A'( ),B'( ),C'( ).

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,抛物线y=ax2+bx过A(4,0),B(1,3)两点,点C、B关于抛物线的对称轴对称,过点B作直线BH⊥x轴,交x轴于点H.
(1)求抛物线的表达式;
(2)直接写出点C的坐标,并求出△ABC的面积;
(3)点P是抛物线上一动点,且位于第四象限,当△ABP的面积为6时,求出点P的坐标;
(4)若点M在直线BH上运动,点N在x轴上运动,当以点C、M、N为顶点的三角形为等腰直角三角形时,请直接写出此时△CMN的面积.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,四边形ABCD是正方形,点E是边BC的中点,∠AEF=90°,且EF交正方形外角的平分线CF于点F.

(1)求证:AE=EF.
(2)(探究1)变特殊为一般:若题中“点E是边BC的中点”变为“点E是BC边上任意一点”,则上述结论是否仍然成立?(填“是”或“否”).
(3)(探究2)在探究1的前提下,若题中结论“AE=EF”与条件“CF是正方形外角的平分线”互换,则命题是否还成立?请给出证明.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,直线y=-x+m与y=nx+4n(n≠0)的交点的横坐标为-2.则下列结论:①m<0,n>0;②直线y=nx+4n一定经过点(-4,0);③m与n满足m=2n-2;④当x>-2时,nx+4n>-x+m,其中正确结论的个数是____个.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在射线AB上顺次取两点C,D,使AC=CD=1,以CD为边作矩形CDEF,DE=2,将射线AB绕点A沿逆时针方向旋转,旋转角记为α(其中0°<α<45°),旋转后记作射线AB′,射线AB′分别交矩形CDEF的边CF,DE于点G,H.若CG=x,EH=y,则下列函数图象中,能反映y与x之间关系的是( )
A.
B.
C.
D.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】由几个相同的边长为1的小立方块搭成的几何体的俯视图如下图,格中的数字表示该位置的小立方块的个数.
(1)请在下面方格纸中分别画出这个向何体的主视图和左视图.

(2)根据三视图;这个组合几何体的表面积为 _________ 个平方单位.(包括底面积)
(3)若上述小立方块搭成的几何体的俯视图不变,各位置的小立方块个数可以改变(总数目不变),则搭成这样的组合几何体中的表面积最大是为 _________ 个平方单位.(包括底面积)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2﹣2x+c的对称轴为直线x=﹣1,顶点为A,与y轴正半轴交点为B,且△ABO的面积为1.
(1)求抛物线的表达式;
(2)若点P在x轴上,且PA=PB,求点P的坐标.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com