
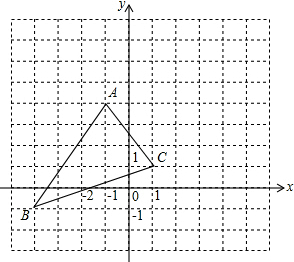
分析 (1)根据横坐标右移加,左移减,纵坐标上移加,下移减即可得出三个顶点的坐标;
(2)根据网格结构分别找到三个顶点的位置,再顺次连接即可得出答案;
(3)将△ABC补全为矩形,然后利用作差法求解即可;
(4)设点D的坐标为(x,2),根据△A1B1D的面积等于△ABC的面积,列出方程$\frac{1}{2}$|x-1|×5=$\frac{19}{2}$,解方程即可.
解答 解:(1)∵A(-1,4)、B(-4,-1)、C(1,1),将△ABC向右平移5个单位长度,再向上平移3个单位长度,
∴A1坐标为(4,7),点B1坐标为(1,2),C1坐标为(6,4);
(2)所画图形如下: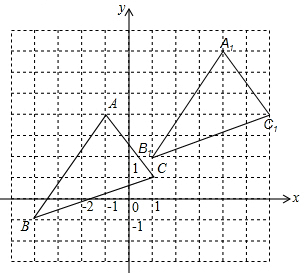
(3)如图,
S△ABC=S矩形EBGF-S△ABE-S△GBC-S△AFC
=5×5-$\frac{1}{2}$×5×3-$\frac{1}{2}$×5×2-$\frac{1}{2}$×2×3
=25-$\frac{15}{2}$-5-3
=$\frac{19}{2}$;
(4)设点D的坐标为(x,2),
∵△A1B1D的面积等于△ABC的面积,
∴$\frac{1}{2}$|x-1|×5=$\frac{19}{2}$,
解得x=$\frac{24}{5}$或-$\frac{14}{5}$.
∴点D的坐标为($\frac{24}{5}$,2)或(-$\frac{14}{5}$,2).
故答案为(4,7),(1,2),(6,4).
点评 本题考查了作图-平移变换,平移的性质,三角形的面积.解答本题的关键是根据平移的特点准确作出图形.


科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积.
如图,双曲线y=$\frac{2}{x}$(x>0)经过四边形OABC的顶点A、C,∠ABC=90°,OC平分OA与x轴正半轴的夹角,AB∥x轴,将△ABC沿AC翻折后得到△AB′C,B′点落在OA上,求四边形OABC的面积.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题

| A. | 61 | B. | 91 | C. | 152 | D. | 169 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
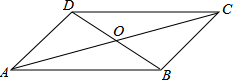 如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )
如图,四边形ABCD的对角线AC、BD相交于点O,则下列条件不能判定四边形ABCD是平行四边形的是( )| A. | AB∥DC,AD∥BC | B. | AB∥DC,∠A=∠C | C. | AO=BO,CO=DO | D. | ∠A=∠C,∠B=∠D |
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com