
【题目】已知![]() 内接于圆
内接于圆![]() ,点
,点![]() 为弧
为弧![]() 上一点,连接
上一点,连接![]() 交
交![]() 于点
于点![]() ,
,![]() .
.
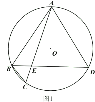
(1)如图1,求证:弧![]() 弧
弧![]() ;
;
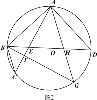
(2)如图2,过![]() 作
作![]() 于点
于点![]() ,交圆
,交圆![]() 点
点![]() ,连接
,连接![]() 交
交![]() 于点
于点![]() ,且
,且![]() ,求
,求![]() 的度数;
的度数;
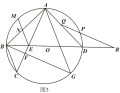
(3)如图3,在(2)的条件下,圆![]() 上一点
上一点![]() 与点
与点![]() 关于
关于![]() 对称,连接
对称,连接![]() ,交
,交![]() 于点
于点![]() ,点
,点![]() 为弧
为弧![]() 上一点,
上一点,![]() 交
交![]() 于点
于点![]() ,交
,交![]() 的延长线于点
的延长线于点![]() ,
,![]() ,
,![]() 的周长为20,
的周长为20,![]() ,求圆
,求圆![]() 半径.
半径.
【答案】(1)见解析;(2)∠CAG=45°;(3)r=![]()
【解析】
(1)证∠ABD=∠ACB可得;
(2)如下图,△AHD绕点A旋转至△ALE处,使得点D与点B重合,证△ALE≌△AHE,利用勾股定理逆定理推导角度;
(3)如下图,延长QR交AB于点T,分别过点N、Q作BD的垂线,交于点V,I,取QU=AE,过点U作UK垂直BD.先证△AEN≌△QUD,再证△NVE≌△RKU,可得到NV=KR=DK,进而求得OB的长.
(1)∵∠CED是△BEC的外角,∴∠CED=∠EBC+∠BCA
∵∠ABC=∠ABD+∠EBC
又∵∠CED=∠ABC
∴∠ABD=∠ACB
∴弧AB=弧AD
(2)如下图,△AHD绕点A旋转至△ALE处,使得点D与点B重合
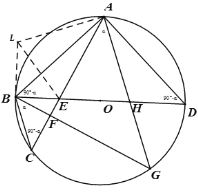
∵△ALB是△AHD旋转所得
∴∠ABL=∠ADB,AL=AH
设∠CAG=a,则∠CBG=a
∵BG⊥AC
∴∠BCA=90°-a,∴∠ADB=∠ABD=90°-a
∴在△BAD中,BAE+∠HAD=180-a-(90°-a)-(90°-a)=a
∴∠LAE=∠EAH=a
∵LA=AH,AE=AE
∴△ALE≌△AHE,∴LE=EH
∵HD=LB,![]()
∴△LBE为直角三角形
∴∠LBE=(90°-a)+(90°-a)=90°,解得:a=45°
∴∠CAG=45°
(3)如下图,延长QR交AB于点T,分别过点N、Q作BD的垂线,交于点V,I,取QU=AE,过点U作UK垂直BD
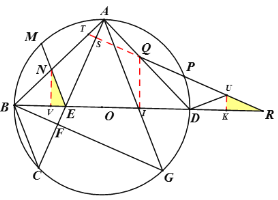
由(2)得∠BAD=90°
∴点O在BD上
设∠R=n,则∠SER=∠BEC=∠MEB=90°-n
∴∠AEN=2n
∵SQ⊥AC
∴∠TAS=∠AQS=∠DQR,AN=QD
∵QU=AE
∴△AEN≌△QUD
∴∠QUD=∠AEN=2n
∴UD=UR=NE,
∵△ANE的周长为20
∴QD+QR=20
在△DQR中,QD=7
∵∠ENR=∠UDK=∠R=n
∴△NVE≌△RKU
∴NV=KR=DK=![]()
∴BN=5
∴BD=12![]() ,OB=6
,OB=6![]()


 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案科目:初中数学 来源: 题型:
【题目】某文化用品商店准备购进甲、乙两种书包进行销售,经调查,乙书包的单价比甲书包贵![]() 元,用
元,用![]() 元购进乙书包的个数与用
元购进乙书包的个数与用![]() 元购进甲书包的个数相等.
元购进甲书包的个数相等.
(1)求甲、乙两种书包的进价分别为多少元?
(2)商户购进甲、乙两种书包共![]() 个进行试销,其中甲书包的个数不少于
个进行试销,其中甲书包的个数不少于![]() 个,且甲书包的个数 的
个,且甲书包的个数 的![]() 倍不大于乙书包的个数,已知甲书包的售价为
倍不大于乙书包的个数,已知甲书包的售价为![]() 元/个,乙书包的售价为
元/个,乙书包的售价为![]() 元/个,且 全部售出,设购进甲书包
元/个,且 全部售出,设购进甲书包![]() 个,求该商店销售这批书包的利润
个,求该商店销售这批书包的利润![]() 与
与![]() 之间的函数关系式,并 写出
之间的函数关系式,并 写出![]() 的取值范围;
的取值范围;
(3)在(2)的条件下,该店将![]() 个书包全部售出后,使用所获的利润又购进
个书包全部售出后,使用所获的利润又购进![]() 个书包捐赠给 贫困地区儿童,这样该商店这批书包共获利
个书包捐赠给 贫困地区儿童,这样该商店这批书包共获利![]() 元.请求出该店第二次进货所选用的进货方案?
元.请求出该店第二次进货所选用的进货方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】超市销售某种儿童玩具,如果每件利润为40元(市场管理部门规定,该种玩具每件利润不能超过60元),每天可售出50件.根据市场调查发现,销售单价每增加2元,每天销售量会减少1件.设销售单价增加![]() 元,每天售出
元,每天售出![]() 件.
件.
(1)请写出![]() 与
与![]() 之间的函数表达式;
之间的函数表达式;
(2)当![]() 为多少时,超市每天销售这种玩具可获利润2250元?
为多少时,超市每天销售这种玩具可获利润2250元?
(3)设超市每天销售这种玩具可获利![]() 元,当
元,当![]() 为多少时
为多少时![]() 最大,最大值是多少?
最大,最大值是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,将二次函数y=x2+2x+1的图象沿x轴翻折,然后向右平移1个单位,再向上平移5个单位,得到二次函数y=ax2+bx+c的图象.函数y=x2+2x+1的图象的顶点为点A.函数y=ax2+bx+c的图象的顶点为点C,两函数图象分别交于B、D两点.
(1)求函数y=ax2+bx+c的解析式;
(2)如图2,连接AD、CD、BC、AB,判断四边形ABCD的形状,并说明理由.
(3)如图3,连接BD,点M是y轴上的动点,在平面内是否存在一点N,使以B、D、M、N为顶点的四边形为矩形?若存在,请求出N点的坐标;若不存在,请说明理由.
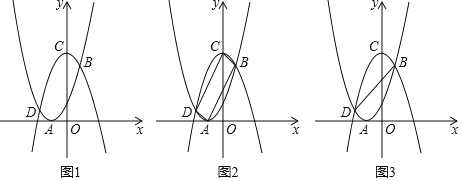
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某校在以“青春心向觉,建功新时代”为主题的校园文化艺术节期间,举办了![]() 合唱,
合唱,![]() 群舞,
群舞,![]() 书法,
书法,![]() 演讲共四个项目的比赛,要求每位学生必须参加且仅参加一项,小红随机调查了部分学生的报名情况,并绘制了下列两幅不完整的统计图,请根据统计图中信息解答下列问题:
演讲共四个项目的比赛,要求每位学生必须参加且仅参加一项,小红随机调查了部分学生的报名情况,并绘制了下列两幅不完整的统计图,请根据统计图中信息解答下列问题:
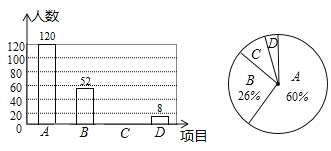
(1)本次调查的学生总人数是多少?扇形统计图中“![]() ”部分的圆心角度数是多少?
”部分的圆心角度数是多少?
(2)请将条形统计图补充完整;
(3)若全校共有1800名学生,请估计该校报名参加书法和演讲比赛的学生共有多少人?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某景点试开放期间,团队收费方案如下:不超过30人时,人均收费120元;超过30人且不超过m(30<m≤100)人时,每增加1人,人均收费降低1元;超过m人时,人均收费都按照m人时的标准.设景点接待有x名游客的某团队,收取总费用为y元.
(1)求y关于x的函数表达式;
(2)景点工作人员发现:当接待某团队人数超过一定数量时,会出现随着人数的增加收取的总费用反而减少这一现象.为了让收取的总费用随着团队中人数的增加而增加,求m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,⊙O的直径AB=26,P是AB上(不与点A、B重合)的任一点,点C、D为⊙O上的两点,若∠APD=∠BPC,则称∠CPD为直径AB的“回旋角”.
(1)若∠BPC=∠DPC=60°,则∠CPD是直径AB的“回旋角”吗?并说明理由;
(2)若![]() 的长为
的长为![]() π,求“回旋角”∠CPD的度数;
π,求“回旋角”∠CPD的度数;
(3)若直径AB的“回旋角”为120°,且△PCD的周长为24+13![]() ,直接写出AP的长.
,直接写出AP的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
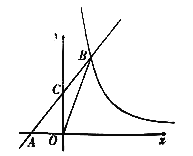
【题目】如图,在平面直角坐标系xOy中,直线y=kx+b(k≠0)与轴交于点A(-2.0),与反比例函数y=![]() (m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(m≠0)的图象交于点B(2,n),连接BO,若S△AOB=4.
(1)求反比例函数和一次函数的表达式:
(2)若直线AB与y轴的交点为C.求△OCB的面积
(3)根据图象,直接写出当x>0时,不等式![]() >kx+b的解集.
>kx+b的解集.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com