
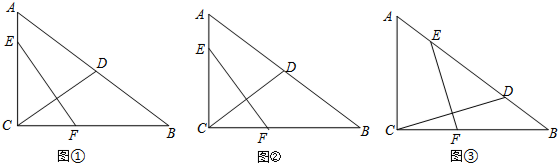
分析 (1)首先在Rt△ABC中,求出AB的长度是多少;然后分两种情况:①当点E和点A重合时;②当点F和点B重合时;分别求出m的最小值和最大值,即可判断出m的取值范围.
(2)首先根据BD=2.5,AB=5,判断出AD=BD=CD=2.5,再根据点C与点D关于对称,判断出CE=DE,CF=DF;然后根据三角形相似的判定方法,分别判断出△ACD∽△CDE,△BCD∽△CDF,即可求出CE、CF的值各是多少;最后在Rt△CEF中,根据勾股定理,求出EF的长度是多少即可.
(3)首先作DG⊥BC,垂足为G,作EH⊥BC,垂足为H,连接DF,根据三角形相似的判定方法,判断出△BGD∽△BCA,求出DG、BG、CG的长度各是多少;然后根据三角形相似的判定方法,判断出△EHF∽△CGD、△EHB∽△ACB,求出FH、EH的长度各是多少;最后在Rt△HEF中,根据勾股定理,求出EF的长度是多少即可.
解答 解:(1)∵∠ACB=90°,AC=3,BC=4,
∴AB=$\sqrt{{AC}^{2}{+BC}^{2}}=\sqrt{{3}^{2}{+4}^{2}}=5$,
∵沿EF折叠,点C与点D重合,
∴EF垂直平分CD,
①当点E和点A重合时,m的值最小,
此时AD=AC=3,
∴m=AB-AD=5-3=2;
②当点F和点B重合时,m的值最大,
此时BD=BC=4,
∴m=4,
综上,可得若折痕EF的两个端点E、F在直角边上,则m的范围为:2≤m≤4;
(2)∵BD=2.5,AB=5,
∴AD=BD=CD=2.5,
∵点C与点D关于对称,
∴CE=DE,CF=DF,
∴∠CAD=∠ECD=∠EDC,
在△ACD和△CDE中,
$\left\{\begin{array}{l}{∠DAC=∠ECD}\\{∠DCA=∠EDC}\end{array}\right.$,
∴△ACD∽△CDE,
∴$\frac{AC}{CD}$=$\frac{AD}{CE}$,
即$\frac{3}{2.5}$=$\frac{2.5}{CE}$,
∴CE=$\frac{25}{12}$,
∵CF=DF,
∴∠DBC=∠FCD=∠FDC,
在△BCD和△CDF中,
$\left\{\begin{array}{l}{∠DBC=∠FCD}\\{∠DCB=∠FDC}\end{array}\right.$,
∴△BCD∽△CDF,
∴$\frac{BC}{CD}=\frac{BD}{CF}$,
即$\frac{4}{2.5}=\frac{2.5}{CF}$,
∴CF=$\frac{25}{16}$,
∴EF=$\sqrt{{CE}^{2}{+CF}^{2}}=\sqrt{{(\frac{25}{12})}^{2}{+(\frac{25}{16})}^{2}}$=$\frac{125}{48}$.
(3)如图③,作DG⊥BC,垂足为G,作EH⊥BC,垂足为H,连接DF, ,
,
∵AC⊥BC,DG⊥BC,
∴AC∥DG,
∴△BGD∽△BCA,
∴$\frac{DG}{AC}$=$\frac{BD}{AB}$=$\frac{BG}{CB}$,
∴$\frac{DG}{3}=\frac{\frac{20}{13}}{5}=\frac{BG}{4}$,
∴DG=$\frac{12}{13}$,BG=$\frac{16}{13}$,
∴CG=BC-BG=4-$\frac{16}{13}$=$\frac{36}{13}$;
在Rt△FDG中,FG2+DG2=DF2,
∴($\frac{36}{13}$-DF)2+($\frac{12}{13}$)2=DF2,
解得DF=$\frac{20}{13}$,
∴CF=DF=$\frac{20}{13}$,
∵∠HEF+∠HFE=90°,∠GCD+∠HFE=90°,
∴∠HEF=∠GCD,
又∵∠EHF=∠CGD=90°,
在△EHF和△CGD中,
$\left\{\begin{array}{l}{∠HEF=∠GCD}\\{∠EHF=∠CGD}\end{array}\right.$,
∴△EHF∽△CGD,
∴$\frac{EH}{CG}$=$\frac{HF}{DG}$,
∴$\frac{EH}{HF}$=$\frac{CG}{DG}$=$\frac{\frac{36}{13}}{\frac{12}{13}}=3$,
设FH=x,则EH=3x,
∵EH⊥BC,AC⊥BC,
∴EH∥AC,
∴△EHB∽△ACB,
∴$\frac{EH}{AC}$=$\frac{HB}{BC}$,
∴$\frac{3x}{3}$=$\frac{x+4-\frac{20}{13}}{4}$,
解得x=$\frac{32}{39}$,
∴EF=$\sqrt{{FH}^{2}{+EH}^{2}}$=$\sqrt{{(\frac{32}{39})}^{2}{+(\frac{32}{13})}^{2}}$=$\frac{32}{39}$$\sqrt{10}$.
故答案为:2≤m≤4.
点评 (1)此题主要考查了几何变换综合题,考查了分析推理能力,考查了空间想象能力,考查了数形结合方法的应用,要熟练掌握.
(2)此题还考查了相似三角形的判定和性质的应用,要熟练掌握.
(3)此题还考查了直角三角形的性质和应用,以及勾股定理的应用,要熟练掌握.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:解答题
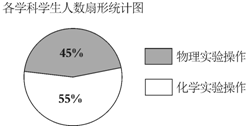 在长沙市初三年级学生考查科目中,对物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A、B、C、D四个等级.现抽取这两种成绩共1 000份进行统计分析,其中A、B、C、D分别表示优秀、良好、合格、不合格四个等级.相关数据统计如下表及图所示.
在长沙市初三年级学生考查科目中,对物理实验操作、化学实验操作成绩进行抽样调查,成绩评定为A、B、C、D四个等级.现抽取这两种成绩共1 000份进行统计分析,其中A、B、C、D分别表示优秀、良好、合格、不合格四个等级.相关数据统计如下表及图所示.| 科目 等级 | A | B | C | D |
| 物理实验操作 | 180 | 210 | 45 | 15 |
| 化学实验操作 | 225 | 250 | 50 | 25 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
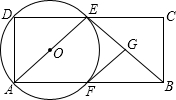 如图,矩形ABCD中,AB=5,AD=3.点E是CD上的动点,以AE为直径的⊙O与AB交于点F,过点F作FG⊥BE于点G.
如图,矩形ABCD中,AB=5,AD=3.点E是CD上的动点,以AE为直径的⊙O与AB交于点F,过点F作FG⊥BE于点G.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,一次函数y=kx-1的图象与x轴交于点A,与反比例函数y=$\frac{3}{x}$(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是( )
如图,一次函数y=kx-1的图象与x轴交于点A,与反比例函数y=$\frac{3}{x}$(x>0)的图象交于点B,BC垂直x轴于点C.若△ABC的面积为1,则k的值是( )| A. | 1 | B. | 2 | C. | 3 | D. | 4 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
 如图,在△ABC中,AB=AC,AD⊥BC于点D,E为边AB上一点,ED=CD,以CE为直径作⊙O,交BC于点F.
如图,在△ABC中,AB=AC,AD⊥BC于点D,E为边AB上一点,ED=CD,以CE为直径作⊙O,交BC于点F.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com