
 如图,在矩形ABCD中,AD=2,AB=3,点E是AD边的中点,点F是射线AB上的一动点,将△AEF沿EF所在的直线翻折得到△A′EF,连接A′C,则A′C的最小值为$\sqrt{10}$-1.
如图,在矩形ABCD中,AD=2,AB=3,点E是AD边的中点,点F是射线AB上的一动点,将△AEF沿EF所在的直线翻折得到△A′EF,连接A′C,则A′C的最小值为$\sqrt{10}$-1. 分析 根据点F是射线AB上的一动点,将△AEF沿EF所在的直线翻折得到△A′EF,可得点A'的运动路径为以E为圆心,AE长为半径的半圆,再根据两点之间线段最短,即可得出当点A'、C、E三点共线时,A′C的长最小,最后根据勾股定理进行计算即可.
解答 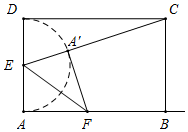 解:当点F在射线AB上移动时,点A'的运动路径为以E为圆心,AE长为半径的半圆(点A'不与点D重合),
解:当点F在射线AB上移动时,点A'的运动路径为以E为圆心,AE长为半径的半圆(点A'不与点D重合),
如图所示,当点A'、C、E三点共线时,A′C的长最小,
∵矩形中,AD=2,AB=3,点E是AD边的中点,
∴DE=AE=1,CD=3,
∴Rt△CDE中,CE=$\sqrt{C{D}^{2}+D{E}^{2}}$=$\sqrt{{3}^{2}+{1}^{2}}$=$\sqrt{10}$,
又∵A'E=AE=$\frac{1}{2}$AD=1,
∴A'C=CE-A'E=$\sqrt{10}$-1,
即A′C的最小值为$\sqrt{10}$-1,
故答案为:$\sqrt{10}$-1.
点评 本题主要考查了折叠问题,解决问题的关键是依据折叠得到点A'的运动轨迹.解题时注意:点A'的运动路径为以E为圆心,AE长为半径的半圆.


 学业测评一课一测系列答案
学业测评一课一测系列答案科目:初中数学 来源: 题型:解答题
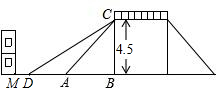 如图是一座人行天桥的示意图,CB⊥DB,天桥的高度CB为4.5米,斜坡AC的坡角为45°,为了方便行人推车过天桥,市政部门决定拆除原斜坡,使新建斜坡DC的坡度i=1:1.8,若D处的左侧需留3米宽的人行道,问距A处7米的建筑物M是否需要拆除?(点B,A,D,M在同一直线上)
如图是一座人行天桥的示意图,CB⊥DB,天桥的高度CB为4.5米,斜坡AC的坡角为45°,为了方便行人推车过天桥,市政部门决定拆除原斜坡,使新建斜坡DC的坡度i=1:1.8,若D处的左侧需留3米宽的人行道,问距A处7米的建筑物M是否需要拆除?(点B,A,D,M在同一直线上)查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知在平面直角坐标系中,已知A(2,3),B(3,5),点P为直线y=x-2上一个动点,当|PB-PA|值最大时,点P的坐标为(-1,-3).
已知在平面直角坐标系中,已知A(2,3),B(3,5),点P为直线y=x-2上一个动点,当|PB-PA|值最大时,点P的坐标为(-1,-3).查看答案和解析>>
科目:初中数学 来源: 题型:选择题
 如图,已知l1∥l2,直角三角板的直角顶点在直线l2上,若∠1=58°,则下列结论错误的是( )
如图,已知l1∥l2,直角三角板的直角顶点在直线l2上,若∠1=58°,则下列结论错误的是( )| A. | ∠3=58° | B. | ∠4=122° | C. | ∠5=52° | D. | ∠2=58° |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com