
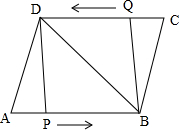
 如图,已知?ABCD中,AD=8cm,AB=10cm,BD=12cm,点P从点A出发,以1cm/s的速度向点B运动,同时点Q从点C出发以相同的速度向点D运动,设运动时间为t.
如图,已知?ABCD中,AD=8cm,AB=10cm,BD=12cm,点P从点A出发,以1cm/s的速度向点B运动,同时点Q从点C出发以相同的速度向点D运动,设运动时间为t.分析 (1)根据平行四边形的性质得AD=BC、∠A=∠C,结合AP=CQ=t,证△APD≌△CQB可得答案;
(2)①先证PBQD是平行四边形,由∠DPB=90°时四边形PBQD为矩形,可得AD2-AP2=BD2-BP2,即82-t2=122-(10-t)2,解之可得;
②先表示出PE=t-1,由PD=PB=10-t时四边形PBQD为菱形,由AD2-AE2=PD2-PE2,即82-12=(10-t)2-(t-1)2,解之可得.
解答 解:(1)由题意知AP=CQ=t,
∵四边形ABCD是平行四边形,
∴AD=BC、∠A=∠C,
在△APD和△CQB中,
∵$\left\{\begin{array}{l}{AD=CB}\\{∠A=∠C}\\{AP=CQ}\end{array}\right.$,
∴△APD≌△CQB(SAS),
∴DP=BQ;
(2)①∵四边形ABCD是平行四边形,
∴AB∥CD,AB=CD=10,AP=CQ=t,
∴DQ∥PB,且DQ=PB=10-t,
∴四边形PBQD是平行四边形,
如图1,
当∠DPB=90°时,四边形PBQD为矩形,
则AD2-AP2=BD2-BP2,即82-t2=122-(10-t)2,
解得:t=1,
∴当t=1时,四边形PBDQ是矩形;
故答案为:1;
②如图2,
过点D作DE⊥AB于点E,
由①知AE=1,
则PE=AP-AE=t-1,
当PD=PB=10-t时,四边形PBQD为菱形,
则AD2-AE2=PD2-PE2,即82-12=(10-t)2-(t-1)2,
解得:t=2,
∴当t=2时,四边形PBDQ是菱形;
故答案为:2.
点评 本题主要考查平行四边形的判定与性质及矩形的判定、菱形的判定,熟练掌握矩形和菱形的判定及勾股定理是解题的关键.


 导学全程练创优训练系列答案
导学全程练创优训练系列答案科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
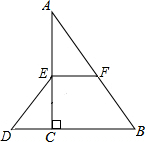 如图,在Rt△ABC中,∠ACB=90°,点E,F分别是边AC,AB的中点,延长BC到点D,使2CD=BC,连接DE.
如图,在Rt△ABC中,∠ACB=90°,点E,F分别是边AC,AB的中点,延长BC到点D,使2CD=BC,连接DE.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
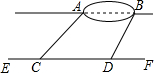 某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.
某兴趣小组想测量位于一池塘两端的A、B之间的距离,组长小明带领小组成员沿着与直线AB平行的道路EF行走,当行走到点C处,测得∠ACF=45°,再向前行走100米到达点D处,测得∠BDF=60°,已知AB与EF之间的距离为60米,求A、B两点的距离.查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | 该抛物线可由抛物线y=ax2向右平移2个单位,向下平移2个单位得到 | |
| B. | 若1<m<n<3,则a>0 | |
| C. | 若1<x0<3,则y0<0 | |
| D. | 不论a取何值,m+n=4 |
查看答案和解析>>
科目:初中数学 来源: 题型:选择题
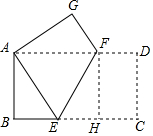 如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )
如图,将长方形ABCD沿直线EF折叠,使顶点C恰好落在顶点A处,已知AB=4cm,AD=8cm,则折痕EF的长为( )| A. | 5cm | B. | $2\sqrt{5}$cm | C. | 2$\sqrt{3}$cm | D. | $3\sqrt{5}$cm |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
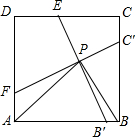 如图,在正方形ABCD中,点E,F分别为CD,AD上的点,点B′、C′分别为边BC、AB上的点,B′E⊥CF于P,连接AP、BP,∠APB=90°.
如图,在正方形ABCD中,点E,F分别为CD,AD上的点,点B′、C′分别为边BC、AB上的点,B′E⊥CF于P,连接AP、BP,∠APB=90°.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com