
【题目】设a,b,c是△ABC的三条边,关于x的方程![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
a=0有两个相等的实数根,方程3cx+2b=2a的根为x=0.
(1)试判断△ABC的形状;
(2)若a,b为方程x2+mx-3m=0的两个根,求m的值.
【答案】(1)∵![]() x2+
x2+![]() x+c-
x+c-![]() a=0有两个相等的实数根,
a=0有两个相等的实数根,
∴△=(![]() )2-4×
)2-4×![]() (c-
(c-![]() a)=0,
a)=0,
整理得a+b-2c="0" ①,
又∵3cx+2b=2a的根为x=0,
∴a="b" ②,
把②代入①得a=c,
∴a=b=c,
∴△ABC为等边三角形;
(2)a,b是方程x2+mx-3m=0的两个根,
∴方程x2+mx-3m=0有两个相等的实数根
∴△=m2-4×(-3m)=0,
即m2+12m=0,
∴m1=0,m2=-12.
当m=0时,原方程的解为x=0(不符合题意,舍去),
∴m=-12.
【解析】
(1)因为方程有两个相等的实数根,即△=0,由△=0可以得到一关于a,c的方程,再结合方程3cx+2b=2a的根为x=0,代入即可得到一关于a,b的方程,联立即可求出a,b,c的关系.
(2)根据(1)中求出a,b的值,可以关于m的方程,解方程即可求出m.
解:![]() ∵
∵![]() 有两个相等的5t实数根,
有两个相等的5t实数根,
∴![]() ,
,
整理得![]() ①,
①,
又∵![]() 的根为
的根为![]() ,
,
∴![]() ②,
②,
把②代入①得![]() ,
,
∴![]() ,
,
∴![]() 为等边三角形;
为等边三角形;
![]() ,
,![]() 是方程
是方程![]() 的两个根,
的两个根,
∴方程![]()
∴![]() ,
,
即![]() ,
,
∴![]() ,
,![]() .
.
当![]() 时,原方程的解为
时,原方程的解为![]() (不符合题意,舍去),
(不符合题意,舍去),
∴![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】如图,将三角形纸片ABC沿AD折叠,使点C落在BD边上的点E处.若BC=8,BE=2.则AB2﹣AC2的值为( )
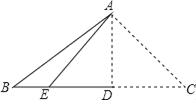
A. 4 B. 6 C. 10 D. 16
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读材料:若![]() ,求m、n的值.
,求m、n的值.
解: ![]() ,
,
![]()
![]() ,
,
![]() ,
,
![]() .
.
根据你的观察,探究下面的问题:
(1)己知![]() ,求
,求![]() 的值.
的值.
(2)已知△ABC的三边长a、b、c都是正整数,且满足![]() ,求边c的最大值.
,求边c的最大值.
(3) 若己知![]() ,求
,求![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】解放中学为了了解学生对新闻、体育、动画、娱乐四类电视节目的喜爱程度,随机抽取了部分学生进行调查(每人限选1项),现将调查结果绘制成如下两幅不完整的统计图,根据图中所给的信息解答下列问题.
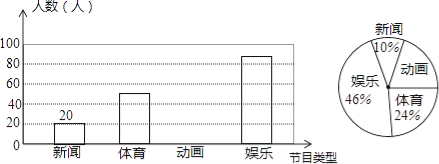
(1)喜爱动画的学生人数和所占比例分别是多少?
(2)请将条形统计图补充完整;
(3)若该校共有学生1000人,依据以上图表估计该校喜欢体育的人数约为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场服装部销售一种名牌衬衫,平均每天可售出![]() 件,每件盈利
件,每件盈利![]() 元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价
元.为了扩大销售,减少库存,商场决定降价销售,经调查,每件降价![]() 元时,平均每天可多卖出
元时,平均每天可多卖出![]() 件.
件.
(1)若商场要求该服装部每天盈利![]() 元,每件衬衫应降价多少元?
元,每件衬衫应降价多少元?
(2)试说明每件衬衫降价多少元时,商场服装部每天盈利最多.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一个自然数的立方,可以分裂成若干个连续奇数的和,例如:![]() ,
,![]() 和
和![]() 分别可以按如图所示的方式“分裂”成2个,3个和4个连续奇数的和,即
分别可以按如图所示的方式“分裂”成2个,3个和4个连续奇数的和,即![]() ,
,![]() ,…,若
,…,若![]() 也按照此规律来进行“分裂”,则
也按照此规律来进行“分裂”,则![]() “分裂”出的奇数中,最大的奇数是( )
“分裂”出的奇数中,最大的奇数是( )



A.39B.41C.43D.45
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知等腰三角形ABC中,AB=AC,点D,E分别在边AB、AC上,且AD=AE,连接BE、CD,交于点F.

(1)求证:∠ABE=∠ACD;
(2)求证:过点A、F的直线垂直平分线段BC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,是用4个全等的直角三角形与1个小正方形镶嵌而成的正方形图案.已知大正方形面积为49,小正方形面积为4,若用![]() ,
,![]() 表示直角三角形的两直角边
表示直角三角形的两直角边![]() ,下列四个说法:①
,下列四个说法:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() ;其中说法正确的是
;其中说法正确的是![]()
![]()

A. ①②B. ①②③C. ①②④D. ①②③④
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在线段AB上取一点C(非中点),分别以AC、BC为边在AB的同侧作等边△ACD和等边△BCE,连接AE交CD于点F,连接BD交CE于点G,AE和BD交于点H.
(1)求证:△ACE≌△DCB
(2)求∠BHE的度数

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com