
【题目】如图,在矩形ABCD中,把∠B,∠D分别翻折,使点B,D分别落在对角线AC上的点E,F处,折痕分别为CM,AN.
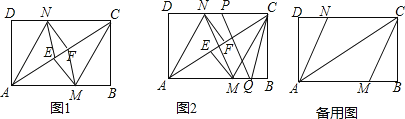
(1)求证:△AND≌△CMB;
(2)连接MF、NE,证明四边形MFNE是平行四边形;四边形MFNE是菱形吗?请说明理由;
(3)点P、Q是矩形的边CD、AB上的两点,连接PQ、CQ、MN,如图2所示,若PQ=CQ,PQ∥MN,且AB=4,BC=3,DN=![]() ,求PC的长度.
,求PC的长度.
【答案】见解析
【解析】
试题分析:(1)根据折叠的性质得出∠DAN=∠NAC,∠BCM=∠ACM,从而根据AD∥BC可得出∠DAN=∠BCM,从而即可判断出△ADN≌△CBM.
(2)连接NE、MF,根据(1)的结论可得出NF=ME,再由∠NFE=∠MEF可判断出NF∥ME,在直角三角形NFE中,NE为斜边,NF为直角边,可判断四边形MFNE不是菱形.
(3)设AC与MN的交点为O,EF=x,作QG⊥PC于G点,首先求出AC=5,根据翻折变换知:AF=CE=3,于是可得AF+(CE﹣EF)=5,可得EF=1,在Rt△NFE中,NO2=NF2+OF2,求出NO的长,即NM=PQ=QC=2NO,PC=2![]() .
.
(1)证明:∵四边形ABCD是正方形,
∴AD=BC,∠B=∠D=90°,
由折叠的性质得出∠DAN=∠NAC,∠BCM=∠ACM,
∵AD∥BC,
∴∠DAC=∠BCA,
∴∠DAN=∠BCM,
在Rt△AND和Rt△CMB中,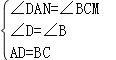 ,
,
∵∴△AND≌△CMB(AAS)
(2)解:由(1)得:△AND≌△CMB,
∴NF=ME,
∵∠NFE=∠MEF,
∴NF∥ME,
∴四边形MFNE是平行四边形,
∵MN与EF不垂直,
∴四边形MFNE不是菱形;
(3)解:设AC与MN的交点为O,EF=x,作QG⊥PC于G点,如图所示:
∵AB=4,BC=3,
∴AC=5,
∵AF=CE=BC=3,
∴2AF﹣EF=AC,即6﹣x=5,
解得:x=1,
∴EF=1,
∴CF=2,
由折叠的性质得:NF=DN=![]() ,
,
∵OE=OF=![]() EF=
EF=![]() ,
,
∴在Rt△NFO中,ON2=OF2+NF2,
∴ON=![]() ,
,
∴MN=2ON=![]() ,
,
∵PQ∥MN,PN∥MQ,
∴四边形MQPN是平行四边形,
∴MN=PQ=![]() ,
,
∵PQ=CQ,
∴△PQC是等腰三角形,
∴PG=CG,
在Rt△QPG中,PG2=PQ2﹣QG2,
∴PG=![]() =1,
=1,
∴PC=2PG=2.



科目:初中数学 来源: 题型:
【题目】下列不能能组成三角形的线段是( )
A. 5cm,3cm,6cmB. 3cm,4cm,5cmC. 2cm,4cm,6cmD. 5cm,6cm,9cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列说法正确的是( )
A.长度相等的弧叫等弧
B.平分弦的直径一定垂直于该弦
C.三角形的外心是三条角平分线的交点
D.不在同一直线上的三个点确定一个圆
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC和△DEF中,AB=DE,∠B=∠E,补充条件后仍不一定能保证△ABC≌△DEF,则补充的这个条件为( )
A. BC=EF B. ∠A=∠D C. AC=DF D. ∠C=∠F
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】△ABC在平面直角坐标系xOy中的位置如图所示.
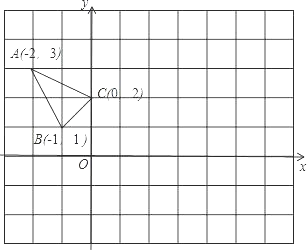
(1)作△ABC关于点C成中心对称的△A1B1C1.
(2)将△A1B1C1向右平移4个单位,作出平移后的△A2B2C2.
(3)在x轴上求作一点P,使PA1+PC2的值最小,并写出点P的坐标(不写解答过程,直接写出结果)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某市实施“限塑令”后,2008年大约减少塑料消耗约4万吨.调查分析结果显示,从2008年开始,五年内该市因实施“限塑令”而减少的塑料消耗量y(万吨)随若时间x(年)逐年成直线上升,y 与x之间的关系如图所示.
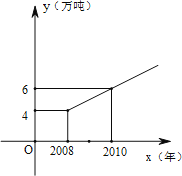
(1)求y与x之间的关系式;
(2)请你估计,该市2011年因实施“限塑令”而减少的塑料消耗量为多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,△ABC的角平分线OB与角平分线OC相交于点O,过点O作MN∥BC,分别交AB、AC于点M、N.
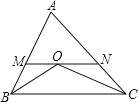
(1)请写出图中所有的等腰三角形;
(2)若AB+AC=14,求△AMN的周长.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com