
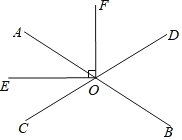
【题目】如图,直线AB、CD相交于点O,OE平分∠AOC,OE⊥OF,∠AOE=32°.
(1)求∠DOB的度数;
(2)OF是∠AOD的角平分线吗?为什么?
【答案】(1)∠DOB=64°;(2)OF是∠AOD的角平分线,理由见解析.
【解析】
(1)根据角平分线的性质可得∠AOC=2∠AOE=64°,再根据对顶角相等即可求∠DOB的度数.
(2)根据垂直的定义得∠EOF=90°,再根据角的和差关系可得∠AOD=2∠AOF,即可得证OF是∠AOD的角平分线.
(1)∵OE平分∠AOC,
∴∠AOC=2∠AOE=64°.
∵∠DOB与∠AOC是对顶角,
∴∠DOB=∠AOC=64°;
(2)∵OE⊥OF,
∴∠EOF=90°,
∴∠AOF=∠EOF﹣∠AOE=58°.
∵∠AOD=180°﹣∠AOC=116°,
∴∠AOD=2∠AOF,
∴OF是∠AOD的角平分线.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】两根木条一根长80cm另一根长60cm,把它们一端重合放在同一直线上,此时两根木条中点的距离是( )
A.10cmB.70cm或10cmC.20cmD.20cm或70cm
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在四张背面完全相同的纸牌A、B、C、D,其中正面分别画有四个不同的几何图形(如图),小华将这4张纸牌背面朝上洗匀后摸出一张,放回洗匀后再摸一张.
(1)用树状图(或列表法)表示两次摸牌所有可能出现的结果(纸牌可用A、B、C、D表示);
(2)求摸出两张纸牌牌面上所画几何图形,既是轴对称图形又是中心对称图形的概率.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一本小说共![]() 页,一位同学第一天看了全书的
页,一位同学第一天看了全书的![]() 少6页,第二天看了剩下的
少6页,第二天看了剩下的![]() 多6页,第三天把剩下的全部看完.
多6页,第三天把剩下的全部看完.
①该同学第一天看了多少页?
②该同学第二天看了多少页?
③若![]() ,则第三天看了多少页?
,则第三天看了多少页?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,M是△ABC的边BC的中点,AN平分∠BAC,BN⊥AN于点N,延长BN交AC于点D,已知AB=10,BC=15,MN=3
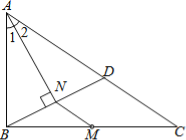
(1)求证:BN=DN;
(2)求△ABC的周长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图是小强洗漱时的侧面示意图,洗漱台(矩形ABCD)靠墙摆放,高AD=80cm,宽AB=48cm,小强身高166cm,下半身FG=100cm,洗漱时下半身与地面成80°(∠FGK=80°),身体前倾成125°(∠EFG=125°),脚与洗漱台距离GC=15cm(点D,C,G,K在同一直线上).
(1)此时小强头部E点与地面DK相距多少?
(2)小强希望他的头部E恰好在洗漱盆AB的中点O的正上方,他应向前或后退多少?
(sin80°≈0.98,cos80°≈0.17, ![]() ≈1.41,结果精确到0.1cm)
≈1.41,结果精确到0.1cm)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一艘渔船位于港口A的北偏东60°方向,距离港口20海里的B处,它沿北偏西37°方向航行至C处突然出现故障,在C处等待救援,B,C之间的距离为10海里,救援船从港口A出发,经过20分钟到达C处,求救援船的航行速度.(sin37°≈0.6,cos37°≈0.8,![]() ≈1.732,结果取整数)
≈1.732,结果取整数)
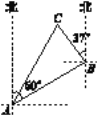
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知正方形![]() 与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
与正方形(点C、E、F、G按顺时针排列),是的中点,连接,.
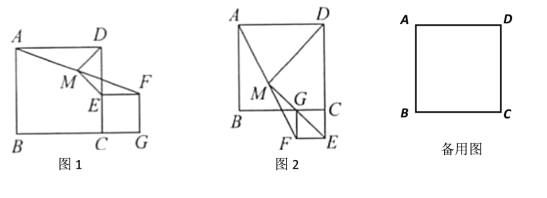
(1)如图1,点![]() 在上,点在的延长线上,
在上,点在的延长线上,
求证:![]() =ME,
=ME,![]() ⊥.ME
⊥.ME
简析: 由是的中点,AD∥EF,不妨延长EM交AD于点N,从而构造出一对全等的三角形,即 ≌ .由全等三角形性质,易证△DNE是 三角形,进而得出结论.
(2)如图2, 在![]() 的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
的延长线上,点在上,(1)中结论是否成立?若成立,请证明你的结论;若不成立,请说明理由.
(3)当AB=5,CE=3时,正方形的顶点C、E、F、G按顺时针排列.若点![]() 在直线CD上,则DM= ;若点E在直线BC上,则DM= .
在直线CD上,则DM= ;若点E在直线BC上,则DM= .
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,BA=BE,∠A=∠E,∠ABE=∠CBD,ED交BC于点F,且∠FBD=∠D.
求证:AC∥BD.
证明:∵∠ABE=∠CBD(已知),
∴∠ABE+∠EBC=∠CBD+∠EBC( )
即∠ABC=∠EBD
在△ABC和△EBD中,
 ,
,
∴△ABC≌△EBD( ),
∴∠C=∠D( )
∵∠FBD=∠D,
∴∠C= (等量代换),
∴AC∥BD( )

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com