
如图,AC为⊙O的直径,AC=4,B、D分别在AC两侧的圆上,∠BAD=60°,BD与AC的交点为E.
(1)求点O到BD的距离及∠OBD的度数;
(2)若DE=2BE,求cos∠OED的值和CD的长.
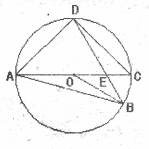
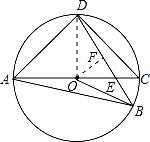
解:(1)作OF⊥BD于点F,连接OD,
∵∠BAD=60°,
∴∠BOD=2∠BAD=120°,
又∵OB=OD,
∴∠OBD=30°,
∵AC为⊙O的直径,AC=4,
∴OB=OD=2.
在Rt△BOF中,∵∠OFB=90°,OB=2,∠OBF=30°,
∴OF=OB•sin∠OBF=2sin30°=1,
即点O到BD的距离等于1.
(2)∵OB=OD,OF⊥BD于点F,
∴BF=DF.
由DE=2BE,设BE=2x,则DE=4x,BD=6x,EF=x,BF=3x.
∵BF=OB•cos30°=![]() ,
,
∴![]() ,EF=
,EF=![]() ,
,
在Rt△OEF中,∠OFE=90°,∵tan∠OED=![]() =
=![]() ,
,
∴∠OED=60°,cos∠OED=![]() ,
,
∴∠BOE=∠OED﹣∠OBD=30°,
∴∠DOC=∠DOB﹣∠BOE=90°,
∴∠C=45°.
∴CD=![]() OC=2
OC=2![]() .
.


 53天天练系列答案
53天天练系列答案科目:初中数学 来源: 题型:
| 2 |

查看答案和解析>>
科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:

| x2+1 |
| (9-x)2+4 |
查看答案和解析>>
科目:初中数学 来源: 题型:
 探索函数y=x+
探索函数y=x+| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
| 1 |
| x |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com