
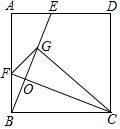
 如图,在正方形ABCD中,AB=6,点E是AD边上一点AE=2,连接BE,点F是AB边上一动点,将△FBC沿CF翻折后,点B恰好落在BE上的点G处,FC交BE于点O,现将△FOG绕点O旋转得到△F′OG′,射线OG′、射线OF′分别交直线AD于点M、N,当△OMN为等腰三角形时GM=$\frac{6}{5}$$\sqrt{13}$.
如图,在正方形ABCD中,AB=6,点E是AD边上一点AE=2,连接BE,点F是AB边上一动点,将△FBC沿CF翻折后,点B恰好落在BE上的点G处,FC交BE于点O,现将△FOG绕点O旋转得到△F′OG′,射线OG′、射线OF′分别交直线AD于点M、N,当△OMN为等腰三角形时GM=$\frac{6}{5}$$\sqrt{13}$. 分析 如图作OH⊥BC于H,HO的延长线交AD于J,作GK⊥AD于K.在Rt△GMK中,求出KG、KM即可解决问题.
解答 解:如图作OH⊥BC于H,HO的延长线交AD于J,作GK⊥AD于K.,连接GM.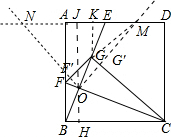
由题意CF⊥BE,∵∠ABE+∠CBE=90°,∠CBE+∠FCB=90°,
∴∠ABE=∠BCF,
在△ABE和△BCF中,
$\left\{\begin{array}{l}{∠EAB=∠CBF}\\{AB=BC}\\{∠ABE=∠BCF}\end{array}\right.$,
∴△ABE≌△BCF,
∴BF=AE=2,∵BC=6,
∴CF=$\sqrt{{2}^{2}+{6}^{2}}$=2$\sqrt{10}$,
∵$\frac{1}{2}$•CF•OB=$\frac{1}{2}$•BF•BC,
∴OB=OG=$\frac{3}{5}$$\sqrt{10}$,
∵△OBH∽△CFB,
∴$\frac{OB}{CF}$=$\frac{OH}{BC}$=$\frac{BH}{BF}$,
∴OH=$\frac{9}{5}$,BH=AJ=JK=$\frac{3}{5}$,
∵BE=CF=2$\sqrt{10}$,
∴EG=BE=BG=$\frac{4}{5}$$\sqrt{10}$,
由$\frac{KG}{AB}$=$\frac{KE}{AE}$=$\frac{EG}{EB}$,可得KE=$\frac{4}{5}$,KG=$\frac{12}{5}$,
∵△MON是等腰直角三角形,
∴OM=ON,∵OJ⊥MN,
∴OJ=JN=JM=$\frac{21}{5}$,
∴KM=$\frac{21}{5}$-$\frac{3}{5}$=$\frac{18}{5}$,
在Rt△GMK中,GM=$\sqrt{K{G}^{2}+K{M}^{2}}$=$\sqrt{(\frac{12}{5})^{2}+(\frac{18}{5})^{2}}$=$\frac{6}{5}$$\sqrt{13}$,
故答案为$\frac{6}{5}$$\sqrt{13}$.
点评 本题考查翻折变换、旋转变换、正方形的性质、全等三角形的判定和性质、等腰直角三角形的性质、平行线的性质、勾股定理、解直角三角形等知识,解题的关键是学会添加常用辅助线,灵活运用相似三角形的性质解决问题,属于中考填空题中的压轴题.


科目:初中数学 来源: 题型:解答题
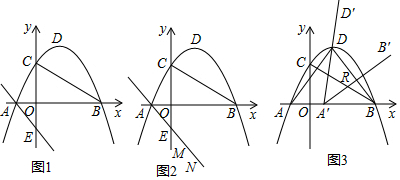
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
| 自来水销售价格 | 污水处理价格 | |
| 每户每月用水量 | 单价:元/吨 | 单价:元/吨 |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
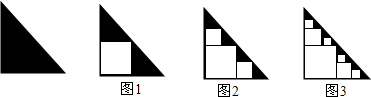
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com