
【题目】如图,已知点E,C在线段BF上,BE=EC=CF,AB∥DE,∠ACB=∠F.
(1)求证:△ABC≌△DEF;
(2)求证:四边形ACFD为平行四边形.

【答案】(1)证明见解析;(2)证明见解析.
【解析】
试题分析: (1)根据平行线得出∠B=∠DEF,求出BC=EF,根据ASA推出两三角形全等即可;(2)根据全等得出AC=DF,推出AC∥DF,得出平行四边形ACFD,推出AD∥CF,MAD=CF,推出AD=CE,AD∥CE,根据平行四边形的判定推出即可.
试题解析:
(1)证明:∵AB∥DE,
∴∠B=∠DEF,
∵BE=EC=CF,
∴BC=EF,
在△ABC和△DEF中
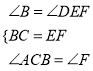
∴△ABC≌△DEF.
(2)证明:∵△ABC≌△DEF,
∴AC=DF,
∵∠ACB=∠F,
∴AC∥DF,
∴四边形ACFD是平行四边形,
∴AD∥CF,AD=CF,
∵EC=CF,
∴AD∥EC,AD=CE,
∴四边形AECD是平行四边形。


科目:初中数学 来源: 题型:
【题目】在眉山市开展城乡综合治理的活动中,需要将![]() 、
、![]() 、
、![]() 三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场
三地的垃圾50立方米、40立方米、50立方米全部运往垃圾处理场![]() 、
、![]() 两地进行处理.已知运往
两地进行处理.已知运往![]() 地的数量比运往
地的数量比运往![]() 地的数量的2倍少10立方米.
地的数量的2倍少10立方米.
(1)求运往两地的数量各是多少立方米?
(2)若![]() 地运往
地运往![]() 地
地![]() 立方米
立方米![]() 为整数),
为整数),![]() 地运往
地运往![]() 地30立方米,
地30立方米,![]() 地运往
地运往![]() 地的数量小于
地的数量小于![]() 地运往
地运往![]() 地的2倍.其余全部运往
地的2倍.其余全部运往![]() 地,且
地,且![]() 地运往
地运往![]() 地不超过12立方米,则
地不超过12立方米,则![]() 、
、![]() 两地运往
两地运往![]() 、
、![]() 两地哪几种方案?
两地哪几种方案?
(3)已知从![]() 、
、![]() 、
、![]() 三地把垃圾运往
三地把垃圾运往![]() 、
、![]() 两地处理所需费用如下表:
两地处理所需费用如下表:
|
|
| |
运往 | 22 | 20 | 20 |
运往 | 20 | 22 | 21 |
在(2)的条件下,请说明哪种方案的总费用最少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,等腰直角三角形AOB的直角顶点A在第四象限,顶点B(0,-2),点C(0,1),点D在边AB上,连接CD交OA于点E,反比例函数![]() 的图像经过点D,若△ADE和△OCE的面积相等,则k的值为___________.
的图像经过点D,若△ADE和△OCE的面积相等,则k的值为___________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矗立在莲花山的邓小平雕像气宇轩昂,这是中国第一座以城市雕塑形式竖立的邓小平雕像。铜像由像体AD和底座CD两部分组成。某校数学课外小组在地面的点B处测得点A的仰角∠ABC=67°,点D的仰角∠DBC=30°,已知CD=2米,求像体AD的高度。(最后结果精确到1米,参考数据:sin67°≈0.92,cos67°≈0.39,tan67°≈2.4,![]() ≈1.7)
≈1.7)

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示的是用棋子摆成的“![]() ”字形图案.
”字形图案.

(1)填写下表:
图案序号 | ① | ② | ③ | ④ | … | ⑩ |
每个图案中棋子的个数 | 5 | 8 | … |
(2)第![]() 个“
个“![]() ”字形图案中棋子的个数为______.(用含
”字形图案中棋子的个数为______.(用含![]() 的代数式表示)
的代数式表示)
(3)第20个“![]() ”字形图案共有棋子多少个?
”字形图案共有棋子多少个?
(4)计算前20个“![]() ”字形图案中棋子的总个数为______
”字形图案中棋子的总个数为______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,OA=3,OC=4![]() ,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
,点B是y轴上一动点,以AC为对角线作平行四边形ABCD.
(1)求直线AC的函数解析式;
(2)设点![]() ,记平行四边形ABCD的面积为
,记平行四边形ABCD的面积为![]() ,请写出
,请写出![]() 与
与![]() 的函数关系式,并求当BD取得最小值时,函数
的函数关系式,并求当BD取得最小值时,函数![]() 的值;
的值;
(3)当点B在y轴上运动,能否使得平行四边形ABCD是菱形?若能,求出点B的坐标;若不能,说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】【问题发现】
(1)如图(1),四边形ABCD中,若AB=AD,CB=CD,则线段BD,AC的位置关系为__________;
【拓展探究】
(2)如图(2),在Rt△ABC中,点F为斜边BC的中点,分别以AB,AC为底边,在Rt△ABC外部作等腰三角形ABD和等腰三角形ACE,连接FD,FE,分别交AB,AC于点M,N.试猜想四边形FMAN的形状,并说明理由;
【解决问题】
(3)如图(3),在正方形ABCD中,AB=2![]() ,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.
,以点A为旋转中心将正方形ABCD旋转60°,得到正方形AB'C'D',请直接写出BD'平方的值.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一段抛物线:y=﹣x(x﹣3)(0≤x≤3),记为C1,它与x轴交于点O,A1;
将C1绕点A1旋转180°得C2,交x轴于点A2;
将C2绕点A2旋转180°得C3,交x轴于点A3;
…
如此进行下去,直至得C13.若P(37,m)在第13段抛物线C13上,则m=_____.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com