
【题目】如图,直线AB、CD、EF相交于点O,且∠AOC=90°,∠AOE=140°,
(1)直线AB与直线______垂直,记作______;
(2)直线AB与直线______斜交,夹角的大小为______;
(3)直线_____与直线______夹角的大小为50°.
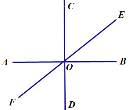
【答案】(1)CD;AB⊥CD;(2)EF;40°;(3)CD;EF
【解析】
(1)根据垂直的定义和垂直的写法即可得出结论;
(2)根据斜交的定义和直线夹角的定义即可得出结论;
(3)求出图中度数为50°的角即可得出结论.
解:(1)∵∠AOC=90°,
∴直线AB与直线CD垂直,记作AB⊥CD
故答案为:CD;AB⊥CD;
(2)∵∠AOE=140°
∴直线AB与直线EF斜交,夹角∠AOF=180°-140°=40°
故答案为:EF;40°;
(3)∵AB⊥CD
∴∠AOD=90°
∵∠AOF=40°
∴∠DOF=∠AOD-∠AOF=50°
∴直线CD与直线EF夹角的大小为50°
故答案为:CD;EF.


科目:初中数学 来源: 题型:
【题目】如图①,在矩形 ABCD 中,动点 E 从点 A 出发,沿 AB→BC 方向运动,当点 E 到达点 C 时 停止运动.过点 E 作 FE⊥AE,交 CD 于 F 点,设点 E 运动路程为 x,FC=y,图②表示 y与 x 的函数关系的大致图像,则矩形 ABCD 的面积是( )
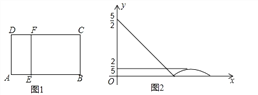
A. ![]() B. 5 C. 6 D.
B. 5 C. 6 D. ![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】阅读下列材料,然后解答后面的问题.
我们知道方程2x+3y=12有无数组解,但在实际生活中我们往往只需要求出其正整数解.例:由2x+3y=12,得![]() ,(x、y为正整数)∴
,(x、y为正整数)∴![]() 则有0<x<6.又
则有0<x<6.又![]() 为正整数,则
为正整数,则![]() 为正整数.
为正整数.
由2与3互质,可知:x为3的倍数,从而x=3,代入![]() .
.
∴2x+3y=12的正整数解为![]()
问题:
(1)请你写出方程2x+y=5的一组正整数解:______;
(2)若![]() 为自然数,则满足条件的x值有______个;
为自然数,则满足条件的x值有______个;
A、2B、3C、4D、5
(3)七年级某班为了奖励学习进步的学生,购买了单价为3元的笔记本与单价为5元的钢笔两种奖品,共花费35元,问有几种购买方案?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知,有理数![]() ,
,![]() ,
,![]() 在数轴上所对应的点分别是
在数轴上所对应的点分别是![]() ,
,![]() ,
,![]() 三点,且
三点,且![]() ,
,![]() ,
,![]() 满足;①
满足;①![]() ;②多项式
;②多项式![]() 是关于
是关于![]() 的二次三项式.
的二次三项式.
(1)![]() ,
,![]() ,
,![]() 的值分别是 (直接写出答案);
的值分别是 (直接写出答案);
(2)若数轴上点![]() ,
,![]() 之间有一动点
之间有一动点![]() ,且点
,且点![]() 对应的数为
对应的数为![]() ,化简
,化简![]() ;
;
(3)若点![]() 在数轴上以每秒1个单位的速度向左运动,同时点
在数轴上以每秒1个单位的速度向左运动,同时点![]() 和点
和点![]() 在数轴上分别以每秒
在数轴上分别以每秒![]() 个单位长度和4个单位长度的速度向右运动(其中
个单位长度和4个单位长度的速度向右运动(其中![]() ),若在整个运动过程中,点
),若在整个运动过程中,点![]() 到点
到点![]() 的距离与点
的距离与点![]() 到点
到点![]() 的距离差始终不变,求运动几秒后点
的距离差始终不变,求运动几秒后点![]() 与点
与点![]() 的距离为13个单位长度.
的距离为13个单位长度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在平面直角坐标系中,矩形OABC的两边OA,OC分别在x轴和y轴上,并且OA=5,OC=3.若把矩形OABC绕着点O逆时针旋转,使点A恰好落在BC边上的A1处,则点C的对应点C1的坐标为( )
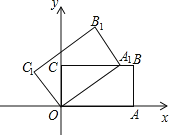
A. (﹣![]() ) B. (﹣
) B. (﹣![]() ) C. (﹣
) C. (﹣![]() ) D. (﹣
) D. (﹣![]() )
)
查看答案和解析>>
科目:初中数学 来源: 题型:
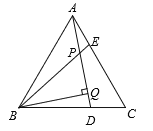
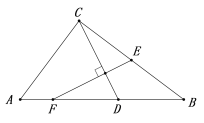
【题目】已知:如图,△ABC是等边三角形,AE=CD,BQ⊥AD于Q,BE交AD于点P.
(1)求证:△ABE≌△CAD;
(2)若PQ=2,BE=5,求PE的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图:在△ABC中,∠ACB =90°,点D在边AB上,AD=AC,点E在BC边上,CE=BD,过点E作EF⊥CD交AB于点F,若AF=2,BC=8,则DF的长为_______
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】对于每个正整数![]() ,设
,设![]() 表示
表示![]() 的末位数字.例如:
的末位数字.例如:![]() (
(![]() 的末位数字),
的末位数字),![]() (
(![]() 的末位数字),
的末位数字),![]() (
(![]() 的末位数字),…则
的末位数字),…则![]() 的值为( )
的值为( )
A.4040B.4038C.0D.4042
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在△ABC中,∠ABC与∠ACB的平分线交于点O,过点O作DE//BC,分别交AB,AC于点D,E,若AB=4,AC=3,则△ADE的周长是_______________。

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com