
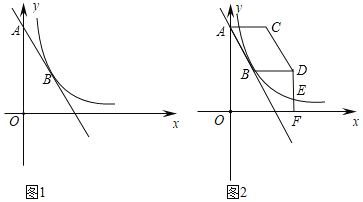
【题目】如图1,在平面直角坐标系中,点A(0,4),B(1,m)都在直线y=﹣2x+b上,反比例函数y=![]() (x>0)的图象经过点B.
(x>0)的图象经过点B.
(1)直接写出m和k的值;
(2)如图2,将线段AB向右平移n个单位长度(n≥0),得到对应线段CD,连接AC,BD.
①在平移过程中,若反比例函数图象与线段AB有交点,求n的取值范围;
②在平移过程中,连接BC,若△BCD是直角三角形,请直接写出所有满足条件n的值.
【答案】(1)m=2,k=2;(2)①0≤n≤![]() ;②n的值为1或5
;②n的值为1或5
【解析】
(1)先将点A坐标代入直线AB的解析式中,求出m,进而求出点B坐标,再将点B坐标代入反比例函数解析式中即可得出结论;
(2)①由将线段AB向右平移n个单位长度,得到A(n,4),把A(n,4)代入y=![]() 中即可得到结论;
中即可得到结论;
②根据平移的性质得到AB∥CD,当∠CBD=90°时,△BCD是直角三角形,当∠BCD=90°,△BCD是直角三角形,根据直角三角形的性质即可得到结论.
(1)∵点A(0,4)在直线y=﹣2x+b上,
∴﹣2×0+b=4,
∴b=4,
∴直线AB的解析式为y=﹣2x+4,
将点B(1,m)代入直线AB的解析式y=﹣2x+4中,得﹣2×1+4=m,
∴b=2,
∴B(1,2),
将B(1,2)在反比例函数解析式y=![]() (x>0)中,得k=xy=1×2=2;
(x>0)中,得k=xy=1×2=2;
(2)①∵将线段AB向右平移n个单位长度,
∴A(n,4),
把A(n,4)代入y=![]() 中,得,4=
中,得,4=![]() ,
,
∴n=![]() ,
,
∴在平移过程中,若反比例函数图象与线段AB有交点,n的取值范围为0≤n≤![]() ;
;
②∵将线段AB向右平移n个单位长度(n≥0),得到对应线段CD,
∴AB∥CD,
∴∠CDB≠90°,
当∠CBD=90°时,△BCD是直角三角形,
∴CB⊥BC,
∴C(1,4),
∴n=1;
当∠BCD=90°,△BCD是直角三角形,
则C(n,4),D(n+1,2),
∵BC2+CD2=BD2,
∴(n﹣1)2+(4﹣2)2+12+(4﹣2)2=n2,
解得:n=5,
综上所述,若△BCD是直角三角形,n的值为1或5.


科目:初中数学 来源: 题型:
【题目】在平面直角坐标系中有两点![]() ,若二次函数
,若二次函数![]() 的图像与线段AB只有一个交点,则( )
的图像与线段AB只有一个交点,则( )
A.![]() 的值可以是
的值可以是![]() B.
B.![]() 的值可以是
的值可以是![]()
C.![]() 的值不可能是-1.2D.
的值不可能是-1.2D.![]() 的值不可能是-1
的值不可能是-1
查看答案和解析>>
科目:初中数学 来源: 题型:
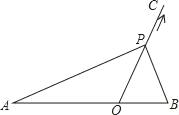
【题目】如图,点O在线段AB上,AO=2,OB=1,OC为射线,且∠BOC=60°,动点P以每秒2个单位长度的速度从点O出发,沿射线OC做匀速运动,设运动时间为t秒.当△ABP是直角三角形时,t的值为( )
A. ![]() B.
B. ![]() C. 1或
C. 1或![]() D. 1或
D. 1或![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(1)某学校“智慧方园”数学社团遇到这样一个题目:
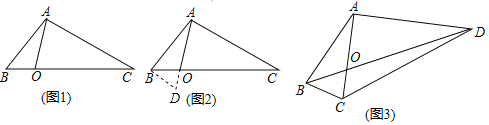
如图1,在△ABC中,点O在线段BC上,∠BAO=30°,∠OAC=75°,AO=![]() ,BO:CO=1:3,求AB的长.
,BO:CO=1:3,求AB的长.
经过社团成员讨论发现,过点B作BD∥AC,交AO的延长线于点D,通过构造△ABD就可以解决问题(如图2).
请回答:∠ADB= °,AB= .
(2)请参考以上解决思路,解决问题:
如图3,在四边形ABCD中,对角线AC与BD相交于点O,AC⊥AD,AO=![]() ,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
,∠ABC=∠ACB=75°,BO:OD=1:3,求DC的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年沈阳国际马拉松赛事设有“马拉松”(A),“半程马拉松”(B),“10公里跑”(C),“迷你马拉松”(D)四个项目,小明和小亮参加了该赛事的志愿者服务工作,组委会将志愿者随机分配到四个项目组,被分配到每个项目组的机会是相同的.
(1)小明被分配到“马拉松”(A)项目组的概率为 ;
(2)利用画树状图或列表法求小明和小亮被分配到同一个项目组进行志愿服务的概率.(项目名称可用字母表示)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在路灯下,小明的身高如图中线段AB所示,他在地面上的影子如图中线段AC所示,小亮的身高如图中线段FG所示,路灯灯泡在线段DE上.

(1)请你确定灯泡所在的位置,并画出小亮在灯光下形成的影子.
(2)如果小明的身高AB=1.6m,他的影子长AC=1.4m,且他到路灯的距离AD=2.1m,求灯泡的高.
查看答案和解析>>
科目:初中数学 来源: 题型:
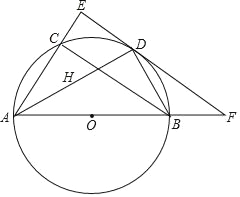
【题目】如图,在直角三角形ABC中,∠ACB=90°,点H是△ABC的内心,AH的延长线和三角形ABC的外接圆O相交于点D,连结DB.
(1)求证:DH=DB;
(2)过点D作BC的平行线交AC、AB的延长线分别于点E、F,已知CE=1,圆O的直径为5.
①求证:EF为圆O的切线;
②求DF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】综合与探究
如图,在平面直角坐标系中,已知抛物线![]() 与
与![]() 轴交于
轴交于![]() 两点(点
两点(点![]() 在点
在点![]() 的右侧),与
的右侧),与![]() 轴交于点
轴交于点![]() ,连接
,连接![]() .
.
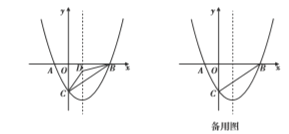
(1)求点![]() 三点的坐标和抛物线的对称轴;
三点的坐标和抛物线的对称轴;
(2)点![]() 为抛物线对称轴上一点,连接
为抛物线对称轴上一点,连接![]() ,
,![]() ,若
,若![]() ,求点
,求点![]() 的坐标;
的坐标;
(3)已知点![]() ,若
,若![]() 是抛物线上一个动点(其中
是抛物线上一个动点(其中![]() ),连接
),连接![]() ,
,![]() ,
,![]() ,求
,求![]() 面积的最大值及此时点
面积的最大值及此时点![]() 的坐标.
的坐标.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知二次函数![]() (其中a,b,c为常数)的图象如图所示,有以下结论:①
(其中a,b,c为常数)的图象如图所示,有以下结论:①![]() ;②
;②![]() ;③
;③![]() ;④关于x的一元二次方程
;④关于x的一元二次方程![]() 有两个不相等的实数根.其中正确结论的番号是( )
有两个不相等的实数根.其中正确结论的番号是( )
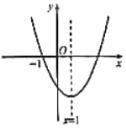
A.①②④B.①③④C.①④D.③④
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com