Question

19．如图，在平面直角坐标系中，∠AOB=90°，OA=OB，若点A的坐标为（-1，4），则点B的坐标为（-4，-1）．

Answer 1

分析 分别过点A和点B作AC⊥y轴，BD⊥y轴，利用已知条件和等腰直角三角形的性质可证明△ACO≌△BDO，则OD和BD的长可求出，进而得到点B的坐标．

解答 解：
分别过点A和点B作AC⊥y轴，BD⊥y轴，
∴∠ACO=∠BDO=90°，
∴∠AOC+∠CAO=90°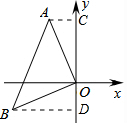
∵∠AOB=90°，
∴∠AOC+∠BOD=90°，
∴∠CAO=∠BOD，
在△ACO和△BDO中，
$\left\{\begin{array}{l}{∠ACO=∠BDO=90°}\\{∠CAO=∠BOD}\\{AO=BO}\end{array}\right.$
∴△ACO≌△BDO（AAS），
∴OD=AC，BD=OC，
∵点A的坐标为（-1，4），
∴OD=AC=1，BD=OC=4，
∴点B的坐标为（-4，-1），
故答案为：（-4，-1）．

点评 本题考查了等腰直角三角形，用到的知识点是等腰直角三角形的性质，全等三角形的判定，能够正确作出辅助线，构造出全等三角形是解题的关键．