
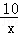 (x>0)的图象上,有一系列点A1、A2、A3、…、An、An+1,若A1的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2.现分别过点A1、A2、A3、…、An、An+1作x轴与y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1= ,S1+S2+S3+…+Sn= .(用n的代数式表示).
(x>0)的图象上,有一系列点A1、A2、A3、…、An、An+1,若A1的横坐标为2,且以后每点的横坐标与它前一个点的横坐标的差都为2.现分别过点A1、A2、A3、…、An、An+1作x轴与y轴的垂线段,构成若干个矩形如图所示,将图中阴影部分的面积从左到右依次记为S1,S2,S3,…,Sn,则S1= ,S1+S2+S3+…+Sn= .(用n的代数式表示).
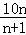
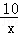 (x>0)的图象上,且每点的横坐标与它前一个点的横坐标的差都为2,
(x>0)的图象上,且每点的横坐标与它前一个点的横坐标的差都为2,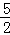 )
)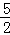 )=5;
)=5;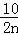 ),An+1(2n+2,
),An+1(2n+2,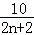 ),
),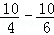 )=
)=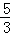 ,
,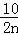
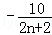 )=
)=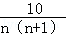 ,(n=1,2,3,…)
,(n=1,2,3,…)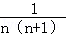 =
=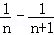 ,
, +
+ +…+
+…+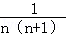 )=10(1
)=10(1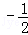
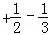
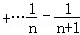 )=
)=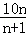 .
.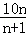 .
.

科目:初中数学 来源:不详 题型:解答题
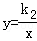 的图象在第一象限内的交点为M,若△OBM的面积为2.
的图象在第一象限内的交点为M,若△OBM的面积为2.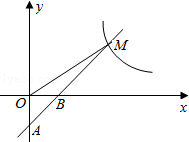
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
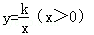 的图象与边BC交于点F.
的图象与边BC交于点F.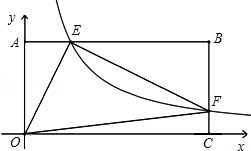
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
 的第一象限的那一支上,AB垂直于y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .
的第一象限的那一支上,AB垂直于y轴于点B,点C在x轴正半轴上,且OC=2AB,点E在线段AC上,且AE=3EC,点D为OB的中点,若△ADE的面积为3,则k的值为 .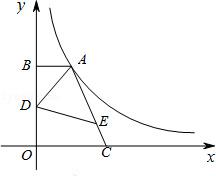
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
 ,y1),B(2,y2)为反比例函数y=
,y1),B(2,y2)为反比例函数y= 图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
图象上的两点,动点P(x,0)在x轴正半轴上运动,当线段AP与线段BP之差达到最大时,点P的坐标是( )
A.( ,0) ,0) | B.(1,0) | C.( ,0) ,0) | D.( ,0) ,0) |
查看答案和解析>>
科目:初中数学 来源:不详 题型:填空题
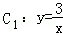 (虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论:
(虚线部分)沿x轴的正方向、向右平移2个单位,得一个新的双曲线C2(实线部分),对于新的双曲线C2,下列结论: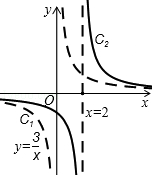
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
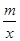 (x>0)的图象上.
(x>0)的图象上.
查看答案和解析>>
科目:初中数学 来源:不详 题型:单选题
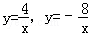 的图象在第一象限,第二象限如图,点P1、P2、P3…P2010在
的图象在第一象限,第二象限如图,点P1、P2、P3…P2010在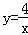 的图象上,它们的横坐标分别是有这样规律的一行数列1,3,5,7,9,11,…,过点P1、P2、P3、…、P2010分别作x轴的平行线,与
的图象上,它们的横坐标分别是有这样规律的一行数列1,3,5,7,9,11,…,过点P1、P2、P3、…、P2010分别作x轴的平行线,与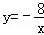 的图象交点依次是Q1、Q2、Q3、…、Q2010,则点Q2010的横坐标是 .
的图象交点依次是Q1、Q2、Q3、…、Q2010,则点Q2010的横坐标是 .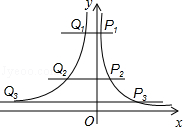
查看答案和解析>>
科目:初中数学 来源:不详 题型:解答题
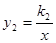 (x>0)的图象交于A、B两点,与y轴交于C点.已知A点的坐标为(2,1),C点的坐标为(0,3).
(x>0)的图象交于A、B两点,与y轴交于C点.已知A点的坐标为(2,1),C点的坐标为(0,3).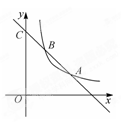
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com