
根据要求将下面题目改编为一道新题.
已知:如图(甲),在等腰梯形ABCD中,AD∥BC,PA=PD.
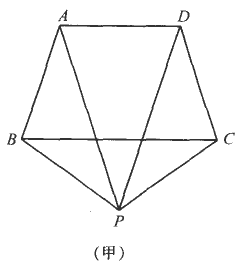
求证:PB=PC.
请你将上述题目的条件“在等腰梯形ABCD中,AD∥BC”改为另一种四边形,其余条件都不变,使结论“PB=PC”仍然成立.再根据改编后的题目画出图形,写出已知和求证,并进行证明.
科目:初中数学 来源:解题升级 解题快速反应一典通 九年级级数学 题型:044
根据要求将下面的题目改编为一道新题.已知:如图,在等腰梯形ABCD中,AD∥BC,P为梯形外一点,PA=PD.求证:PB=PC.
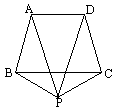
请你将上述题目的条件“在等腰梯形ABCD中,AD∥BC”改为另一种四边形,其余条件都不变,使结论“PB=PC”仍然成立,再根据改编后的题目画出图形,写出已知和求证,并证明.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com