
【题目】计算:
①已知:a+![]() =1+
=1+![]() ,求a2+
,求a2+![]() 的值.
的值.
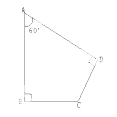
②如图,四边形ABCD中∠A=60°,∠B=∠D=90°,AB=2,CD=1,求四边形ABCD的面积。
【答案】①![]() ;②
;②![]()
【解析】试题分析:①把 a+![]() =1+
=1+![]() 的两边分别平方,进一步整理得出a2+
的两边分别平方,进一步整理得出a2+![]() 的值.
的值.
②延长AD、BC交于E,根据直角三角形两锐角互余求出∠E=30°,然后根据直角三角形30°角所对的直角边等于斜边的一半求出AE、CE,再利用勾股定理列式求出BE、DE,然后根据四边形的面积等于两个直角三角形的面积的差列式计算即可得解.
试题解析:
①∵a+![]() =1+
=1+![]() ,
,
∴(a+![]() )2=(1+
)2=(1+![]() )2,
)2,
∴a2+![]() +2=11+2
+2=11+2![]() ,
,
∴a2+![]() =9+2
=9+2![]() ;
;
②如图,延长AD、BC交于E.
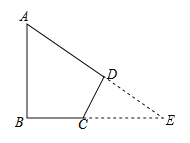
∵∠B=90°,∠A=60°,
∴∠E=90°-60°=30°,
在Rt△ABE和Rt△CDE中,∵AB=2,CD=1,
∴AE=2AB=2×4,CE=2CD=2×1=2,
由勾股定理得,BE=![]() ,
,
DE=![]() ,
,
∴S四边形ABCD=![]()
=![]()
=![]() .
.


 名校课堂系列答案
名校课堂系列答案科目:初中数学 来源: 题型:
【题目】解答题。
(1)计算:18+42÷(﹣2)﹣(﹣3)2×5.
(2)化简求值:(5xy﹣8x2)﹣(﹣12x2+4xy),其中x=﹣0.5,y=2.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某向在静水中的航行速度为每小时a千米,水流速度为每小时b千米,轮船顺水航行的速度是________,逆水航行的速度_______________.
查看答案和解析>>
科目:初中数学 来源: 题型:
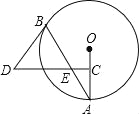
【题目】如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若CD=15,BE=10,tanA=![]() ,求⊙O的直径.
,求⊙O的直径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】(2016山东潍坊第18题)在平面直角坐标系中,直线l:y=x﹣1与x轴交于点A1,如图所示依次作正方形A1B1C1O、正方形A2B2C2C1、…、正方形AnBnCnCn﹣1,使得点A1、A2、A3、…在直线l上,点C1、C2、C3、…在y轴正半轴上,则点Bn的坐标是 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在等腰直角△ABC中,∠ACB=90°,AC=BC,直线MN经过点C,且AD⊥MN于D,BE⊥MN于E.
(1)求证:△ADC≌△CEB;
(2)求证:AD+BE=DE;
(3)当直线MN绕点C旋转到图2的位置时,试问DE、AD、BE具有怎样的等量关系?请写出这个等量关系,并加以说明.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在正方形ABCD中,M是BC边(不含端点B、C)上任意一点,P是BC延长线上一点,N是∠DCP的平分线上一点.若∠AMN=90°,求证:AM=MN.
下面给出一种证明的思路,你可以按这一思路证明,也可以选择另外的方法证明.
证明:在边AB上截取AE=MC,连ME.
正方形ABCD中,∠B=∠BCD=90°,AB=BC.
∴∠NMC=180°—∠AMN—∠AMB
=180°—∠B—∠AMB
=∠MAB=∠MAE.
(下面请你完成余下的证明过程)
(2)若将(1)中的“正方形ABCD”改为“正三角形ABC”(如图2),N是∠ACP的平分线上一点,则当∠AMN=60°时,结论AM=MN是否还成立?请说明理由.
(3)若将(1)中的“正方形ABCD”改为“正![]() 边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
边形ABCD…X”,请你作出猜想:当∠AMN=°时,结论AM=MN仍然成立.(直接写出答案,不需要证明)
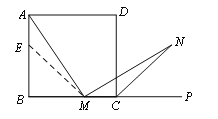
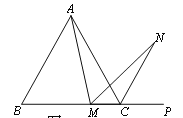
图1 图2
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com