
【题目】如图,已知AO为Rt△ABC的角平分线,∠ACB=90°,以O为圆心,OC为半径的圆分别交AO,BC于点D,E,连接ED并延长交AC于点F.
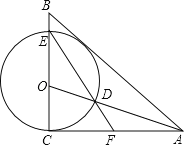
(1)求证:AB是⊙O的切线;
(2)当![]() 时,求
时,求![]() 的值;
的值;
(3)在(2)的条件下,若⊙O的半径为4,求![]() 的值.
的值.
【答案】(1)证明见解析;(2)![]() ;(3)
;(3)![]() 的值为
的值为![]() .
.
【解析】
(1)作OG⊥AB于点G,运用角平分线的性质证明;
(2)根据线段比例关系,设未知数表示线段AC、BC的长度,运用勾股定理和切线长定理,求出BG,易证△![]() ∽△
∽△![]() ,根据相似三角形对应线段成比例求出OG,进而分别求出CE
,根据相似三角形对应线段成比例求出OG,进而分别求出CE
和BE,据此求解;
(3)由CE=![]() =2×4,求出
=2×4,求出![]() 的值,从而求出AC、BC,运用勾股定理求出AO,则AD=AO-OD,证明△DFA∽△CDA,根据对应线段成比例求出AF,则CF=AC-AF,进而求出
的值,从而求出AC、BC,运用勾股定理求出AO,则AD=AO-OD,证明△DFA∽△CDA,根据对应线段成比例求出AF,则CF=AC-AF,进而求出![]() .
.
(1)证明:作OG⊥AB于点G.
∵∠ACB=90°,
∴BC⊥AC,
∵AO为Rt△ABC的角平分线,
∴OG=OC
∴AB是⊙O的切线;
(2)∵![]()
∴设![]() ,
,![]() ,
,
∵∠ACB=90°
∴![]() ,
,
∵AB、AC是⊙O的切线,
∴![]()
∴![]() ,
,
∵![]() ,
,![]() =90°,
=90°,
∴![]() ∽
∽![]() ,
,
∴![]() ,即
,即![]() ,
,
∴![]() ,
,
∴![]() ,
,![]() ,
,
∴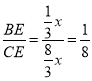 ;
;
(3)连接CD.
由(2)得CE=![]() =2×4,
=2×4,
解得![]() =3,
=3,
∴AC=12,BC=9,
∴AO![]() ,
,
AD=AO﹣OD=4![]() ﹣4,
﹣4,
∵CE是![]() O的直径,
O的直径,
∴∠CDE=90°,
∵∠ACB=90°,
∴∠CDE=∠ACB=90°,
∴∠CED+∠ECD=∠ECD+∠ACD=90°,
∴∠CED=∠ACD,
∵OD=OE,
∴∠CED=∠ODE,
又∵∠ODE=∠ADF,
∴∠ADF=∠ACD,
又∵∠DAF=∠CAD
∴△DFA∽△CDA,
∴![]() ,
,
即![]() ,
,
解得 AF![]() ,
,
CF![]() 12﹣
12﹣![]() ,
,
∴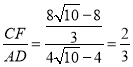 ,
,
故求得![]() 的值为
的值为![]() .
.



 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】已知抛物线y=ax2-bx+3的对称轴是直线x=-1
(1)求证:2a+b=0;
(2)若关于x的方程ax2-bx-8=0的一个根是4,求方程的另一个根.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果直线l把△ABC分割后的两个部分面积相等,且周长也相等,那么就把直线l叫做△ABC的“完美分割线”,已知在△ABC中,AB=AC,△ABC的一条“完美分割线”为直线l,且直线l平行于BC,若AB=2,则BC的长等于_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某食品厂生产一种半成品食材,成本为2元/千克,每天的产量P(百千克)与销售价格x(元/千克)满足函数关系式p=![]() x+8.从市场反馈的信息发现,该食材每天的市场需求量q(百千克)与销售价格x(元/千克)满足一次函数关系,部分数据如表:
x+8.从市场反馈的信息发现,该食材每天的市场需求量q(百千克)与销售价格x(元/千克)满足一次函数关系,部分数据如表:
销售价格x(元/千克) | 2 | 4 | …… | 10 |
市场需求量q(百千克) | 12 | 10 | …… | 4 |
已知按物价部门规定销售价格x不低于2元/千克且不高于10元/千克,
(1)直接写出q与x的函数关系式,并注明自变量x的取值范围;
(2)当每天的产量小于或等于市场需求量时,这种食材能全部售出;当每天的产量大于市场需求量时,只能售出市场需求的量,而剩余的食材由于保质期短作废弃处理;
①当每天的食材能全部售出时,求x的取值范围;
②求厂家每天获得的利润y(百元)与销售价格x的函数关系式;
(3)在(2)的条件下,当x为多少时,y有最大值,并求出最大利润.
查看答案和解析>>
科目:初中数学 来源: 题型:
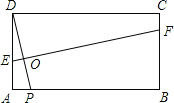
【题目】如图,在矩形ABCD中,AB=3,AD=1,点P在线段AB上运动,设AP=![]() ,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.
,现将纸片折叠,使点D与点P重合,得折痕EF(点E、F为折痕与矩形边的交点),再将纸片还原.
(1)当![]() =0时,折痕EF的长为 ;当点E与点A重合时,折痕EF的长为 ;
=0时,折痕EF的长为 ;当点E与点A重合时,折痕EF的长为 ;
(2)请写出使四边形EPFD为菱形的![]() 的取值范围,并求出当
的取值范围,并求出当![]() =2时菱形的边长;
=2时菱形的边长;
(3)令EF2=![]() ,当点E在AD、点F在BC上时,写出
,当点E在AD、点F在BC上时,写出![]() 与
与![]() 的函数关系式.当
的函数关系式.当![]() 取最大值时,判断△EAP与△PBF是否相似?若相似,求出
取最大值时,判断△EAP与△PBF是否相似?若相似,求出![]() 的值;若不相似,请说明理由.温馨提示:用草稿纸折折看,或许对你有所帮助哦!
的值;若不相似,请说明理由.温馨提示:用草稿纸折折看,或许对你有所帮助哦!
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】中华文明,源远流长;中华汉字,寓意深广.为了传承中华民族优秀传统文化,我市某中学举行“汉字听写”比赛,赛后整理参赛学生的成绩,将学生的成绩分为A,B,C,D四个等级,并将结果绘制成如图所示的条形统计图和扇形统计图,但均不完整.

请你根据统计图解答下列问题:
(1)参加比赛的学生共有____名;
(2)在扇形统计图中,m的值为____,表示“D等级”的扇形的圆心角为____度;
(3)组委会决定从本次比赛获得A等级的学生中,选出2名去参加全市中学生“汉字听写”大赛.已知A等级学生中男生有1名,请用列表法或画树状图法求出所选2名学生恰好是一名男生和一名女生的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】好街坊橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
进价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共 30 台,用去了 5520 元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过 8850 元的资金采购电饭煲和电压锅共 50 台,且电饭煲的利润不少于电压锅的利润的![]() ,问橱具店有哪几种进货方案?并说明理由;
,问橱具店有哪几种进货方案?并说明理由;
(3)在(2)的条件下,请你通过计算判断,哪种进货方案橱具店赚钱最多?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,等腰三角形ABC中,当顶角∠A的大小确定时,它的对边(即底边BC)与邻边(即腰AB或AC)的比值也就确定,我们把这个比值记作T(A),即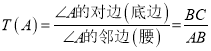 ,如T(60°)=1.
,如T(60°)=1.
(1)理解巩固:T(90°)= ,T(120°)= ;
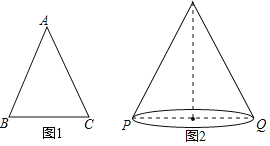
(2)学以致用:如图2,圆锥的母线长为9,底面直径PQ=8,一只蚂蚁从P点这沿着圆锥的侧面爬行到点Q.
①求圆锥侧面展开图的扇形圆心角的数;
②求蚂蚁爬行的最短路径长(精确到0.1).(参考数据:T(160°)≈1.97,T(80°)≈1.29,T(40°)≈0.68)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com