
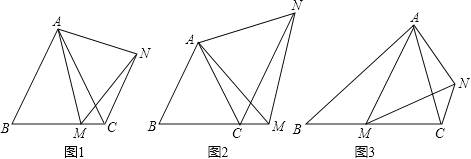
【题目】【提出问题】
(1)如图1,在等边△ABC中,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等边△AMN,连结CN.求证:∠ABC=∠ACN.
【类比探究】
(2)如图2,在等边△ABC中,点M是BC延长线上的任意一点(不含端点C),其它条件不变,(1)中结论∠ABC=∠ACN还成立吗?请说明理由.
【拓展延伸】
(3)如图3,在等腰△ABC中,BA=BC,点M是BC上的任意一点(不含端点B、C),连结AM,以AM为边作等腰△AMN,使顶角∠AMN=∠ABC.连结CN.试探究∠ABC与∠ACN的数量关系,并说明理由.
【答案】见解析
【解析】解:(1)证明:∵△ABC、△AMN是等边三角形,∴AB=AC,AM=AN,∠BAC=∠MAN=60°。
∴∠BAM=∠CAN。
∵在△BAM和△CAN中,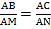 ,
,
∴△BAM≌△CAN(SAS)。∴∠ABC=∠ACN。
(2)结论∠ABC=∠ACN仍成立。理由如下:
∵△ABC、△AMN是等边三角形,∴AB=AC,AM=AN,∠BAC=∠MAN=60°。
∴∠BAM=∠CAN。
∵在△BAM和△CAN中,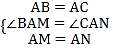 ,
,
∴△BAM≌△CAN(SAS)。∴∠ABC=∠ACN。
(3)∠ABC=∠ACN。理由如下:
∵BA=BC,MA=MN,顶角∠ABC=∠AMN,∴底角∠BAC=∠MAN。
∴△ABC∽△AMN。∴![]() 。
。
又∵∠BAM=∠BAC﹣∠MAC,∠CAN=∠MAN﹣∠MAC,∴∠BAM=∠CAN.
∴△BAM∽△CAN。∴∠ABC=∠ACN。
(1)利用SAS可证明△BAM≌△CAN,继而得出结论。
(2)也可以通过证明△BAM≌△CAN,得出结论,和(1)的思路完全一样。
(3)首先得出∠BAC=∠MAN,从而判定△ABC∽△AMN,得到![]() ,根据∠BAM=∠BAC﹣
,根据∠BAM=∠BAC﹣
∠MAC,∠CAN=∠MAN﹣∠MAC,得到∠BAM=∠CAN,从而判定△BAM∽△CAN,得出结论。


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】泗县某童装专卖店在销售中发现,一款童装每件进价为![]() 元,利润为
元,利润为![]() 元时,每天可售出
元时,每天可售出![]() 件,为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量增加利润,经市场调查发现,如果每件童装降价
件,为了迎接“六一”儿童节,商店决定采取适当的降价措施,以扩大销售量增加利润,经市场调查发现,如果每件童装降价![]() 元,那么平均每天可售出
元,那么平均每天可售出![]() 件.
件.
(1)设每件童装降价![]() 元,每天可售出 件,每件盈利 元,若商家平均每天能赢利
元,每天可售出 件,每件盈利 元,若商家平均每天能赢利![]() 元,每件童装应降价多少元?根据题意,列出方程 .
元,每件童装应降价多少元?根据题意,列出方程 .
(2)利用配方法解答(1)中所列方程.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】从三角形(不是等腰三角形)一个顶点引出一条射线与对边相交,顶点与交点之间的线段把这个三角形分割成两个小三角形,如果分得的两个小三角形中一个为等腰三角形,另一个与原三角形相似,我们把这条线段叫做这个三角形的完美分割线.
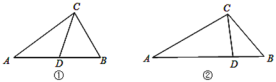
(1)如图①,在△ABC中,CD为角平分线,∠A=40°,∠B=60°,求证:CD是△ABC的完美分割线;
(2)如图②,在△ABC中,AC=2,BC=![]() ,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
,CD是△ABC的完美分割线,且△ACD是以CD为底边的等腰三角形,求完美分割线CD的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在Rt△ABC中,AB=AC,OB=OC,∠A=90°,∠MON=α,分别交直线AB、AC于点M、N.
(1)如图1,当α=90°时,求证:AM=CN;
(2)如图2,当α=45°时,问线段BM、MN、AN之间有何数量关系,并证明;
(3)如图3,当α=45°时,旋转∠MON,问线段之间BM、MN、AN有何数量关系?并证明.
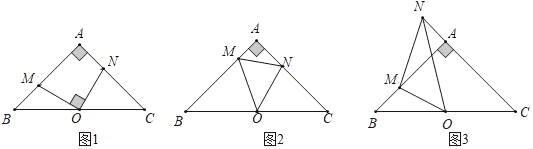
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,将矩形纸片ABCD(AD>AB)沿BD折叠,点C落在点C′处.
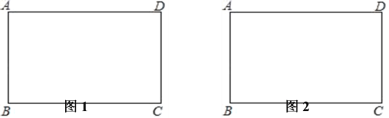
(1)连接BD,请用直尺和圆规在图1中作出点C′;(不写作法,保留作图痕迹)
(2)若BC′与AD相交于点E,EB与ED的数量关系是 ;连接AC′,则AC′与BD的位置关系是 ;
(3)在(2)的条件下,若AB=4,AD=8,求BE的长.(提示:(2)、(3)两题可以在图2中作出草图完成)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,将矩形ABCD的一个角翻折,使得点D恰好落在BC边上的点G处,折痕为EF,若EB为∠AEG的平分线,EF和BC的延长线交于点H.下列结论中:①∠BEF=90°;②DE=CH;③BE=EF;④△BEG和△HEG的面积相等;⑤若![]() ,则
,则![]() .以上命题,正确的有( )
.以上命题,正确的有( )
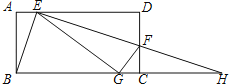
A.2个B.3个C.4个D.5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图(1),![]() 为等腰三角形,
为等腰三角形,![]() ,
,![]() 点是底边
点是底边![]() 上的一个动点,
上的一个动点,![]() ,
,![]() .
.
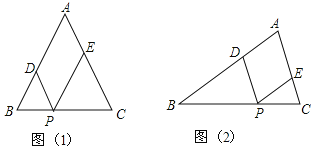
(1)用![]() 表示四边形
表示四边形![]() 的周长为 ;
的周长为 ;
(2)点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形,请说明理由;
是菱形,请说明理由;
(3)如果![]() 不是等腰三角形图(2),其他条件不变,点
不是等腰三角形图(2),其他条件不变,点![]() 运动到什么位置时,四边形
运动到什么位置时,四边形![]() 是菱形(不必说明理由).
是菱形(不必说明理由).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】用适当的方法解下列一元二次方程
(1) (2x-1)2=25
(2) 3x2-6x-1=0
(3) x2-4x-396=0
(4) (2-3x)+(3x-2)2=0
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】![]() 是指空气中直径小于或等于
是指空气中直径小于或等于![]() 的颗粒物,它对人体健康和大气环境造成不良影响,下表是根据《全国城市空气质量报告》中的部分数据制作的统计表.根据统计表回答下列问题,
的颗粒物,它对人体健康和大气环境造成不良影响,下表是根据《全国城市空气质量报告》中的部分数据制作的统计表.根据统计表回答下列问题,

(1)2018年7~12月![]() 平均浓度的中位数为
平均浓度的中位数为 ![]() ;
;
(2)“扇形统计图”和“折线统计图”中,更能直观地反映2018年7~12月![]() 平均浓度变化过程和趋势的统计图是 ;
平均浓度变化过程和趋势的统计图是 ;
(3)某同学观察统计表后说:“2018年7~12月与2017年同期相比,空气质量有所改善”,请你用一句话说明该同学得出这个结论的理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com