
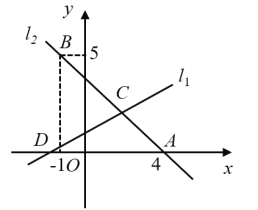
【题目】如图,直线![]() 的解析式为
的解析式为![]() ,且
,且![]() 与
与![]() 轴交于点
轴交于点![]() ,直线
,直线![]() 经过定点
经过定点![]() 、
、![]() ,直线
,直线![]() 与
与![]() 交于点
交于点![]() .
.
(1)求直线![]() 的解析式;
的解析式;
(2)求![]() 的面积;
的面积;
(3)在![]() 轴上是否存在一点
轴上是否存在一点![]() ,使
,使![]() 的周长最短?若存在,请求出点
的周长最短?若存在,请求出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
【答案】(1)![]() ;(2)6;(3)存在,
;(2)6;(3)存在,![]()
【解析】
(1)首先根据题意得出直线![]() 经过定点
经过定点![]() 、
、![]() 的坐标,然后利用待定系数法求出解析式即可;
的坐标,然后利用待定系数法求出解析式即可;
(2)根据两直线的解析式求出点D、点C的坐标,然后进一步得出![]() 的底与高,由此进一步计算即可;
的底与高,由此进一步计算即可;
(3)根据题意得出点C关于![]() 轴的对称点
轴的对称点![]() ,再利用待定系数法求出过点(2,2)和点
,再利用待定系数法求出过点(2,2)和点![]() 的直线的解析式,根据题意分析可知点E在该直线上,由此进一步求出答案即可.
的直线的解析式,根据题意分析可知点E在该直线上,由此进一步求出答案即可.
(1)设直线![]() 的解析式是
的解析式是![]() ,
,
∵直线![]() 图象过A(4,0),B(1,5),
图象过A(4,0),B(1,5),
∴![]() ,
,
解得:![]() ,
,
∴直线![]() 的解析式是:
的解析式是:![]() ;
;
(2)在![]() 中,令
中,令![]() ,解得:
,解得:![]() ,
,
则![]() 的坐标是
的坐标是![]() ,
,
解方程组 得
得![]() ,
,
则![]() 的坐标是
的坐标是![]() ,
,
∴![]() 的底为6,高为2,
的底为6,高为2,
则![]() ;
;
(3)存在;
![]() 关于
关于![]() 轴的对称点是
轴的对称点是![]() ,
,
则设经过点![]() 和点
和点![]() 的直线所对应的函数解析式是
的直线所对应的函数解析式是![]() ,
,
则![]() ,
,
解得 ,
,
则直线为:![]() ,
,
令![]() ,解得:
,解得:![]() ,则
,则![]() 的坐标是
的坐标是![]() ,
,
![]() 当
当![]() 点坐标为
点坐标为![]() 时,
时,![]() 的周长最短.
的周长最短.


 特高级教师点拨系列答案
特高级教师点拨系列答案 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案科目:初中数学 来源: 题型:
【题目】如图1,点C在线段AB上,(点C不与A、B重合),分别以AC、BC为边在AB同侧作等边三角形ACD和等边三角形BCE,连接AE、BD交于点P.
(观察猜想)
①AE与BD的数量关系是 ;
②∠APD的度数为 .
(数学思考)
如图2,当点C在线段AB外时,(1)中的结论①、②是否仍然成立?若成立,请给予证明;若不成立,请你写出正确结论再给予证明;
(拓展应用)
如图3,点E为四边形ABCD内一点,且满足∠AED=∠BEC=90°,AE=DE,BE=CE,对角线AC、BD交于点P,AC=10,则四边形ABCD的面积为 .

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,点O是正方形ABCD两对角线的交点. 分别延长OD到点G,OC到点E,使OG=2OD,OE=2OC,然后以OG、OE为邻边作正方形OEFG,连接AG,DE.
(1)求证:DE⊥AG;
(2)正方形ABCD固定,将正方形OEFG绕点O逆时针旋转![]() 角(0°<
角(0°< ![]() <360°)得到正方形
<360°)得到正方形![]() ,如图2.
,如图2.
①在旋转过程中,当∠![]() 是直角时,求
是直角时,求![]() 的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)
的度数;(注明:当直角边为斜边一半时,这条直角边所对的锐角为30度)
②若正方形ABCD的边长为1,在旋转过程中,求![]() 长的最大值和此时
长的最大值和此时![]() 的度数,直接写出结果不必说明理由.
的度数,直接写出结果不必说明理由.
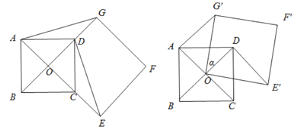
图1 图2
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一次函数y=kx+b与反比例函数y=![]() 的图象相交于A(2,4)、B(-4,n)两点.
的图象相交于A(2,4)、B(-4,n)两点.
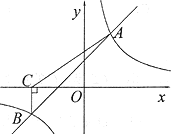
(1)分别求出一次函数与反比例函数的表达式;
(2)根据所给条件,请直接写出不等式kx+b>![]() 的解集 ;
的解集 ;
(3)过点B作BC⊥x轴,垂足为点C,连接AC,求S△ABC.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】为有效解决交通拥堵问题,营造路网微循环,某市决定对一条长![]() 的道路进行改造拓宽.为了尽量减轻施工对城市交通造成的影响,实际施工时,每天改造道路的长度比原计划增加
的道路进行改造拓宽.为了尽量减轻施工对城市交通造成的影响,实际施工时,每天改造道路的长度比原计划增加![]() ,结果提前
,结果提前![]() 天完成任务,求实际每天改造道路的长度与实际施工天数.嘉琪同学根据题意列出方程
天完成任务,求实际每天改造道路的长度与实际施工天数.嘉琪同学根据题意列出方程![]() ,则方程中未知数
,则方程中未知数![]() 所表示的量是( )
所表示的量是( )
A.实际每天改造道路的长度B.原计划每天改造道路的长度
C.原计划施工的天数D.实际施工的天数
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,在平面直角坐标系中,直线y1=2x+4分别与x轴,y轴交于A,B两点,以线段OB为一条边向右侧作矩形OCDB,且点D在直线y2=﹣x+b上,若矩形OCDB的面积为20,直线y1=2x+4与直线y2=﹣x+b交于点P.则P的坐标为( )
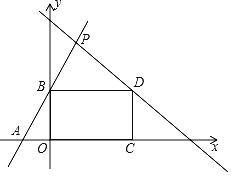
A.(2,8)B.![]() C.
C.![]() D.(4,12)
D.(4,12)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在ABCD中,∠BAD的平分线交CD于点E,交BC的延长线于 点F,连接BE,∠F=45°.
(1)求证:四边形ABCD是矩形;(2)若AB=14,DE=8,求sin∠AEB的值.
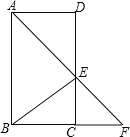
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】甲、乙两所医院分别有一男一女共4名医护人员支援湖北武汉抗击疫情.
(1)若从甲、乙两医院支援的医护人员中分别随机选1名,则所选的2名医护人员性别相同的概率是 ;
(2)若从支援的4名医护人员中随机选2名,用列表或画树状图的方法求出这2名医护人员来自同一所医院的概率.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,抛物线![]() 与y轴交于点D(0,3).
与y轴交于点D(0,3).
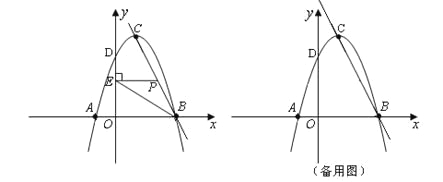
(1)直接写出c的值;
(2)若抛物线与x轴交于A、B两点(点B在点A的右边),顶点为C点,求直线BC的解析式;
(3)已知点P是直线BC上一个动点,
①当点P在线段BC上运动时(点P不与B、C重合),过点P作PE⊥y轴,垂足为E,连结BE.设点P的坐标为(x,y),△PBE的面积为s,求s与x的函数关系式,写出自变量x的取值范围,并求出s的最大值;
②试探索:在直线BC上是否存在着点P,使得以点P为圆心,半径为r的⊙P,既与抛物线的对称轴相切,又与以点C为圆心,半径为1的⊙C相切?如果存在,试求r的值,并直接写出点P的坐标;如果不存在,请说明理由.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com