
【题目】如图,AB∥CD,点E,F分别在AB,CD上,连接EF,∠AEF,∠CFE的平分线交于点G,∠BEF,∠DFE的平分线交于点H.易证∠EHF=∠EGF=∠GEH=90°,从而可知四边形EGFH是矩形.
小明继续进行了探索,过G作MN∥EF,分别交AB,CD于点M,N,过H作PQ∥EF,分别交AB,CD于点P,Q,得到四边形MNQP,此时,他猜想四边形MNQP是菱形,请在下列框中补全他的证明思路.
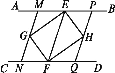
由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形.要证平行四边形MNQP是菱形,只要证MN=NQ.由已知条件_____,MN∥EF,可得NG=NF,故只要证GM=FQ,即证△MGE≌△QFH.易证_____,_____,故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,_____,即可得证.
【答案】FG平分∠CFE GE=FH ∠GME=∠FQH ∠GEF=∠EFH
【解析】
利用菱形的判定方法首先得出要证MNQP是菱形,只要证MN=NQ,再证∠MGE=∠QFH得出即可
由AB∥CD,MN∥EF,PQ∥EF,易证四边形MNQP是平行四边形,
要证MNQP是菱形,只要证MN=NQ,由已知条件:FG平分∠CFE,MN∥EF,
故只要证GM=FQ,即证△MGE≌△QFH,易证GE=FH、∠GME=∠FQH.
故只要证∠MGE=∠QFH,易证∠MGE=∠GEF,∠QFH=∠EFH,∠GEF=∠EFH,即可得证;
故答案为:FG平分∠CFE,GE=FH、∠GME=∠FQH,∠GEF=∠EFH.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:
【题目】如图,在![]() 中,
中,![]() ,
,![]() ,点
,点![]() 是斜边
是斜边![]() 的中点.点
的中点.点![]() 从点
从点![]() 出发以
出发以![]() 的速度向点
的速度向点![]() 运动,点
运动,点![]() 同时从点
同时从点![]() 出发以一定的速度沿射线
出发以一定的速度沿射线![]() 方向运动,规定当点
方向运动,规定当点![]() 到终点
到终点![]() 时停止运动.设运动的时间为
时停止运动.设运动的时间为![]() 秒,连接
秒,连接![]() 、
、![]() .
.
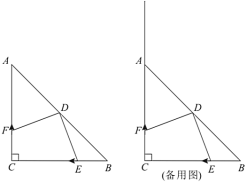
(1)填空:![]() ______
______![]() ;
;
(2)当![]() 且点
且点![]() 运动的速度也是
运动的速度也是![]() 时,求证:
时,求证:![]() ;
;
(3)若动点![]() 以
以![]() 的速度沿射线
的速度沿射线![]() 方向运动,在点
方向运动,在点![]() 、点
、点![]() 运动过程中,如果存在某个时间
运动过程中,如果存在某个时间![]() ,使得
,使得![]() 的面积是
的面积是![]() 面积的两倍,请你求出时间
面积的两倍,请你求出时间![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在一条平坦的公路旁边建造了A,B两栋住房,这两栋住房与小明所就读的西湖中学在同一条直线上,如图,已知A栋住房有6层,每层高4 m;B栋住房共3层,每层也是4 m,且A,B两栋楼相距30 m,小明家住在A栋楼的第5层,放学后,小明从学校向这两栋楼走来.
问:(1)小明离B栋楼多远时,他才能完全看不到他家的那层楼房?
(2)小明要想完全看到他家的那层楼房,他离B栋楼的距离要满足什么条件(小明的身高不计)?

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】下列图形都是由同样大小的菱形按照一定规律所组成的,其中第①个图形中一共有2个空心菱形,第②个图形中一共有5个空心菱形,第③个图形中一共有11个空心菱形,…,按此规律排列下去,第⑨个图形中空心菱形的个数为( )

A.68B.76C.86D.104
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,△ABC中,∠ACB=90°,∠B=30°,AD是角平分线,DE⊥AB于E,AD、CE相交于点H,则图中的等腰三角形有( )
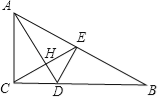
A. 2个 B. 3个 C. 4个 D. 5个
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】矩形ABCD的对角线相交于点O,∠COE=45°,过点C作CE⊥BD于点E,
(1)如图1,若CB=1,求△CED的面积;
(2)如图2,过点O作OF⊥DB于点O,OF=OD,连接FC,点G是FC中点,连接GE,求证:DC=2GE.
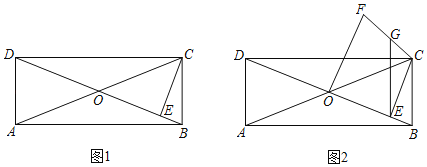
查看答案和解析>>
科目:初中数学 来源: 题型:
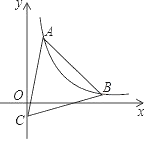
【题目】如图,△ABC是等边三角形,顶点C在y轴的负半轴上,点A(1,![]() ),点B在第一象限,经过点A的反比例函数y=
),点B在第一象限,经过点A的反比例函数y=![]() (x>0)的图象恰好经过顶点B,则△ABC的边长为_____.
(x>0)的图象恰好经过顶点B,则△ABC的边长为_____.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】先仔细阅读材料,再尝试解决问题:我们在求代数式![]() 的最大或最小值时,通过利用公式
的最大或最小值时,通过利用公式![]() 对式子作如下变形:
对式子作如下变形:
![]() ,
,
因为![]() ,
,
所以![]() ,
,
因此![]() 有最小值2,
有最小值2,
所以,当![]() 时,
时,![]() ,
,![]() 的最小值为2.
的最小值为2.
同理,可以求出![]() 的最大值为7.
的最大值为7.
通过上面阅读,解决下列问题:
(1)填空:代数式![]() 的最小值为______________;代数式
的最小值为______________;代数式![]() 的最大值为______________;
的最大值为______________;
(2)求代数式![]() 的最大或最小值,并写出对应的
的最大或最小值,并写出对应的![]() 的取值;
的取值;
(3)求代数式![]() 的最大或最小值,并写出对应的
的最大或最小值,并写出对应的![]() 、
、![]() 的值.
的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
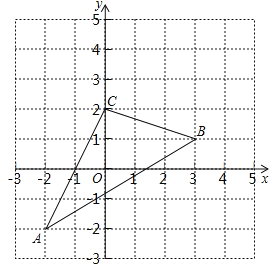
【题目】如图,△ABC在直角坐标系中.
(1)若把△ABC向上平移2个单位,再向左平移1个单位得到△A1B1C1,画出△A1B1C1,并写出点A1,B1,C1的坐标;
(2)求△ABC的面积.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com