
【题目】等腰Rt△ABC中,∠BAC=90°,AB=AC,点A、点B分别是y轴、x轴上两个动点,直角边AC交x轴于点D,斜边BC交y轴于点E;

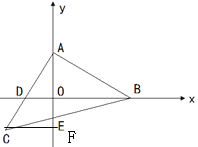
(1)如图(1),已知C点的横坐标为-1,直接写出点A的坐标;
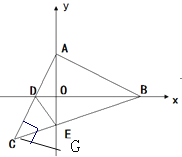
(2)如图(2), 当等腰Rt△ABC运动到使点D恰为AC中点时,连接DE,求证:∠ADB=∠CDE;
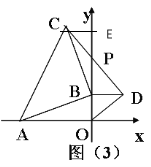
(3)如图(3), 若点A在x轴上,且A(-4,0),点B在y轴的正半轴上运动时,分别以OB、AB为直角边在第一、二象限作等腰直角△BOD和等腰直角△ABC,连结CD交y轴于点P,问当点B在y轴的正半轴上运动时,BP的长度是否变化?若变化请说明理由,若不变化,请求出BP的长度.
【答案】(1)A(0,1);(2)证明见解析;(3)BP的长度不变;理由见解析.
【解析】
试题分析:(1)过点C作![]() 轴于点F,易证
轴于点F,易证![]() ,∴CF=OA=1,∴A(0,1);
,∴CF=OA=1,∴A(0,1);
(2)过点C作![]() 交y轴于点G,易证
交y轴于点G,易证![]() ,则可得CG=AD=CD,由于∠ADB=∠CGA,
,则可得CG=AD=CD,由于∠ADB=∠CGA,
∠DCE=∠GCE=45°,可证![]() ,则∠CDE=∠AGC,∴∠ADB=∠CDE;
,则∠CDE=∠AGC,∴∠ADB=∠CDE;
![]()
![]() (3)过点C作CE⊥y轴于点E,∵∠BAC=90°,∴∠CBE+∠ABO=90°,可证△CBE≌△BAO,∴CE=BO,BE=AO=4,∵BD=BO,∴CE=BD.可证△CPE≌△DPB.∴BP=EP=2 .
(3)过点C作CE⊥y轴于点E,∵∠BAC=90°,∴∠CBE+∠ABO=90°,可证△CBE≌△BAO,∴CE=BO,BE=AO=4,∵BD=BO,∴CE=BD.可证△CPE≌△DPB.∴BP=EP=2 .
试题解析:
(1)如图,过点C作![]() 轴于点F,易证
轴于点F,易证![]() (AAS),
(AAS),
∴CF=OA=1,
∴A(0,1);
(2)如图,过点C作![]() 交y轴于点G,则
交y轴于点G,则![]() (ASA),
(ASA),
∴CG=AD=CD,∠ADB=∠CGA,
∵∠DCE=∠GCE=45°,
∴![]() (SAS),
(SAS),
∴∠CDE=∠AGC,
∴∠ADB=∠CDE;
(4)BP的长度不变,理由如下:
过点C作CE⊥y轴于点E,
∵∠BAC=90°,
∴∠CBE+∠ABO=90°,
∵∠BAO+∠ABO=90°,
∴∠CBE=∠BAO.
∵∠CEB=∠AOB=90°,AB=AC,
∴△CBE≌△BAO(AAS),
![]() ∴CE=BO,BE=AO=4,
∴CE=BO,BE=AO=4,
∵BD=BO,∴CE=BD.
∵∠CEP=∠DBP=90°, ∠CPE=∠DPB,
∴△CPE≌△DPB(AAS).
![]() ∴BP=EP=2 .
∴BP=EP=2 .


 第1卷单元月考期中期末系列答案
第1卷单元月考期中期末系列答案科目:初中数学 来源: 题型:
【题目】某商场用24000元购入一批空调,然后以每台3000元的价格销售,因天气炎热,空调很快售完;商场又以52000元的价格再次购入该种型号的空调,数量是第一次购入的2倍,但购入的单价上调了200元,售价每台也上调了200元.
(1)商场第一次购入的空调每台进价是多少元?
(2)商场既要尽快售完第二次购入的空调,又要在这两次空调销售中获得的利润率不低于22%,打算将第二次购入的部分空调按每台九五折出售,最多可将多少台空调打折出售?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,一个商人要建一个矩形的仓库,仓库的两边是住房墙,另外两边用![]() 长的建筑材料围成,且仓库的面积为
长的建筑材料围成,且仓库的面积为![]() .
.

![]() 求这矩形仓库的长;
求这矩形仓库的长;
![]() 有规格为
有规格为![]() 和
和![]() (单位:
(单位:![]() )的地板砖单价分别为
)的地板砖单价分别为![]() 元/块和
元/块和![]() 元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用一种规格的地板砖费用较少?
元/块,若只选其中一种地板砖都恰好能铺满仓库的矩形地面(不计缝隙),用一种规格的地板砖费用较少?
查看答案和解析>>
科目:初中数学 来源: 题型:
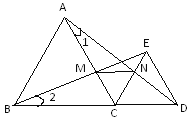
【题目】如图,点C为线段BD上的点,分别以BC,CD为边作等边三角形ABC和等边三角形ECD,连接BE交AC于点M,连接AD交CE于点N,连接MN.试说明:(1)![]() ;(2)
;(2)![]() 为等边三角形.
为等边三角形.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知等腰三角形△ABC,BC边上的高恰好等于BC边长的一半,则∠BAC的度数是( )
A.75°B.90°或75°C.90°或 75°或15°D.75°或15°或60°
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】在初中数学学习阶段,我们常常会利用一些变形技巧来简化式子,解答问题.
材料一:在解决某些分式问题时,倒数法是常用的变形技巧之一,所谓倒数法,即把式子变成其倒数形式,从而运用约分化简,以达到计算目的.
例:已知:![]() ,求代数式x2+
,求代数式x2+![]() 的值.
的值.
解:∵![]() ,∴
,∴![]() =4
=4
即![]() =4∴x+
=4∴x+![]() =4∴x2+
=4∴x2+![]() =(x+
=(x+![]() )2﹣2=16﹣2=14
)2﹣2=16﹣2=14
材料二:在解决某些连等式问题时,通常可以引入参数“k”,将连等式变成几个值为k的等式,这样就可以通过适当变形解决问题.
例:若2x=3y=4z,且xyz≠0,求![]() 的值.
的值.
解:令2x=3y=4z=k(k≠0)
则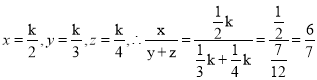
根据材料回答问题:
(1)已知![]() ,求x+
,求x+![]() 的值.
的值.
(2)已知![]() ,(abc≠0),求
,(abc≠0),求![]() 的值.
的值.
(3)若![]() ,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
,x≠0,y≠0,z≠0,且abc=7,求xyz的值.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的弦,D为半径OA的中点,过D作CD⊥OA交弦AB于点E,交⊙O于点F,且BC是⊙O的切线.
(1)求证:CE=CB;
(2)连接AF,BF,求∠ABF的正弦值;
(3)如果CD=15,BE=10,sinA=![]() ,求⊙O的半径.
,求⊙O的半径.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com