
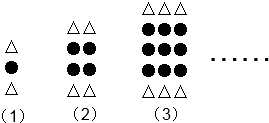
分析 (1)根据题意,求出图中两种不同“符号”的个数和,即可表示出图(3)的“完美多项式”,据此解答即可.
(2)首先根据二元一次方程的求解方法,求出a、b的值各是多少;然后表示出图(8)的一个“完美多项式”,再把求出的a、b的值代入,求出图(8)的一个“完美多项式”的值为多少即可.
解答 解:(1)∵图(3)中“●”、“△”的个数分别为9个、6个,
∴图(3)的“完美多项式”可表示为:9a+6b.
(2)∵图(1)、图(2)的“完美多项式”值分别为-9、-12,
∴$\left\{\begin{array}{l}{a+2b=-9}\\{4a+4b=-12}\end{array}\right.$
解得$\left\{\begin{array}{l}{a=3}\\{b=-6}\end{array}\right.$
∴图(8)的一个“完美多项式”值为:
8a×8+8b×2
=64a+16b
=64×3+16×(-6)
=192-96
=96
即图(8)的一个“完美多项式”值为96.
故答案为:9a+6b,96.
点评 此题主要考查了图形的变化类问题,要熟练掌握,解答此类问题的关键是首先应找出图形哪些部分发生了变化,是按照什么规律变化的,通过分析找到各部分的变化规律后直接利用规律求解.探寻规律要认真观察、仔细思考,善用联想来解决这类问题.


 阅读快车系列答案
阅读快车系列答案科目:初中数学 来源: 题型:填空题
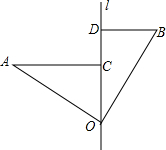 如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D.已知AC=6,BD=4,则CD=2.
如图,∠AOB=90°,OA=OB,直线l经过点O,分别过A、B两点作AC⊥l交l于点C,BD⊥l交l于点D.已知AC=6,BD=4,则CD=2.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:解答题
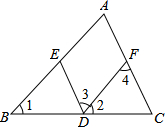 如图,已知∠1=∠2,∠A=∠3,AC与ED平行吗?填空并填写适当的理由.
如图,已知∠1=∠2,∠A=∠3,AC与ED平行吗?填空并填写适当的理由.查看答案和解析>>
科目:初中数学 来源: 题型:填空题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
 已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③$\frac{AF}{AG}$=$\frac{AC}{AB}$;④$\frac{DF}{CF}$=$\frac{EG}{BG}$,其中正确的有①③④(填上你认为所有正确结论的序号).
已知,△ABC中,BE⊥AC于G,CD⊥AB于F,BA=BE,CA=CD,以下结论:①∠D=∠E;②DF=GE;③$\frac{AF}{AG}$=$\frac{AC}{AB}$;④$\frac{DF}{CF}$=$\frac{EG}{BG}$,其中正确的有①③④(填上你认为所有正确结论的序号).查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com