
【题目】已知二次函数y=(x﹣m)2+2(x﹣m)(m为常数)
(1)求证:不论m为何值,该函数的图象与x轴总有两个不同的公共点;
(2)当m取什么值时,该函数的图象关于y轴对称?
【答案】(1)见解析;(2)当m=1时,该函数的图象关于y轴对称.
【解析】
(1)若证明二次函数与x轴总有两个不同的公共点,只需令y=0,得到一元二次方程(x﹣m)2+2(x﹣m)=0,计算方程的判别式b2﹣4ac>0即可;
(2)若二次函数的图象关于y轴对称,则对称轴x=﹣![]() =0,计算即可得到m的值.
=0,计算即可得到m的值.
(1)证明:令y=0,则(x﹣m)2+2(x﹣m)=0,即x2+(2﹣2m)x+m2﹣2m=0,
∵△=(2﹣2m)2﹣4×1×(m2﹣2m)=4>0,
∴方程x2+(2﹣2m)x+m2﹣2m=0有两个不相等的实数根,
∴不论m为何值,该函数的图象与x轴总有两个不同的公共点;
(2)二次函数y=(x﹣m)2+2(x﹣m)=x2+(2﹣2m)x+m2﹣2m,
∵函数的图象关于y轴对称,
∴x=﹣![]() =0,
=0,
解得m=1,
∴当m=1时,该函数的图象关于y轴对称.


 优生乐园系列答案
优生乐园系列答案科目:初中数学 来源: 题型:
【题目】毛泽东在《沁园春·雪》中提到五位历史名人:秦始皇、汉武帝、唐太宗、宋太祖、成吉思汗,小红将这五位名人简介分别写在五张完全相同的知识卡片上.
(1)小哲从中随机抽取一张,求卡片上介绍的人物是唐太宗的概率;
(2)用树状图或列表法求小哲从中随机抽取两张,卡片上介绍的人物均是汉朝以后出生的概率.(注:唐太宗、宋太祖、成吉思汗均是汉朝以后出生)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,反比例函数![]() (x>0)的图象与直线
(x>0)的图象与直线![]() 相交于点A,与直线y=kx(k≠0)相交于点B,若△OAB的面积为18,则k的值为_______________.
相交于点A,与直线y=kx(k≠0)相交于点B,若△OAB的面积为18,则k的值为_______________.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是

A.(0,0)B.(0,1)C.(0,2)D.(0,3)
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】已知![]() 是等腰三角形,
是等腰三角形,![]() ,
,![]() ,点
,点![]() 在边
在边![]() 上,点
上,点![]() 在边
在边![]() 上(点
上(点![]() 不与所在线段端点重合),
不与所在线段端点重合),![]() ,连接
,连接![]() ,射线
,射线![]() ,延长
,延长![]() 交射线
交射线![]() 于点
于点![]() ,点
,点![]() 在直线
在直线![]() 上,且
上,且![]() .
.
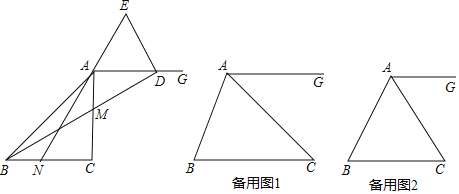
(1)如图,当![]() 时,请直接写出
时,请直接写出![]() 与
与![]() 的关系:_____;
的关系:_____;![]() 与
与![]() 的位置关系:_____.
的位置关系:_____.
(2)当![]() ,其他条件不变时,
,其他条件不变时,![]() 的度数是多少?(用含
的度数是多少?(用含![]() 的代数式表示)
的代数式表示)
(3)若![]() 是等边三角形,
是等边三角形,![]() ,
,![]() 是
是![]() 边上的三等分点,直线
边上的三等分点,直线![]() 与直线
与直线![]() 交于点
交于点![]() ,求线段
,求线段![]() 的长.
的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
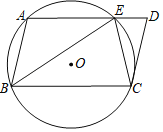
【题目】如图,在ABCD中,过A、B、C三点的⊙O交AD于点E,连接BE、CE,BE=BC.
(1)求证:△BEC∽△CED;
(2)若BC=10,DE=3.6,求⊙O的半径.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,数轴上的点A、B、C、D、E表示连续的五个整数,对应的数分别为a、b、c、d、e。
(1)若a+e=0,直接写出代数式b+c+d的值为_____;
(2)若a+b=7,先化简,再求值:![]() ;
;
(3)若a+b+c+d+e=5,数轴上的点M表示的实数为m,且满足MA+ME>12,则m的范围是____。
![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】2019年春节期间,兰州市开展了以“精致兰州志愿同行”为主题的系列志愿服务活动.金老师和程老师积极参加志愿者活动,当时有下列四个志愿者工作岗位供他们选择:
①“送温暖”活动岗位:为困难家庭打扫卫生,为留守儿童提供学业辅导;(分别用![]() ,
,![]() 表示)
表示)
②“送平安”活动岗位:消防安全常识宣传,人员密集场所维护秩序.(分别用![]() ,
,![]() 表示)
表示)
(1)金老师从四个岗位中随机选取一个报名,恰好选择“送温暖”活动岗位的概率是多少?
(2)若金老师和程老师各随机从四个活动岗位中选一个报名,请用树状图或列表法求出他们恰好都选择同一个岗位的概率.
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com