练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情

    由5个相同的正方体组成的几何体如图所示，则它的主视图是（   ）

     



    B

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：


    若，则＝__________

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    在四边形ABCD中，对角线AC、BD相交于点O，设锐角∠AOB＝α，将△DOC

    按逆时针方向旋转得到△D′OC′（0°＜旋转角＜90°）连接AC′、BD′，AC′与BD′相交于点M．

    （1）当四边形ABCD为矩形时，如图1．求证：△AOC′≌△BOD′．

    （2）当四边形ABCD为平行四边形时，设AC＝kBD，如图2．

    ①猜想此时△AOC′与△BOD′有何关系，证明你的猜想；

    ②探究AC′与BD′的数量关系以及∠AMB与α的大小关系，并给予证明．

    B
     
     

    图2
     
     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知，求的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    已知关于的一元二次方程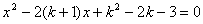有两个不相等的实数根．

    （1）求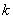的取值范围；

    （2）当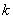取最小的整数时，求抛物线  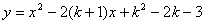    的顶点坐标以及它与轴的交点坐标；

    （3）将(2)中求得的抛物线在轴下方的部分沿轴翻折到轴上方，图象的其余部分不变，得到一个新图象．请你画出这个新图象，并求出新图象与直线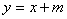有三个不同公共点时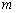的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


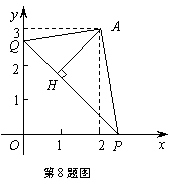
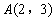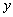     如图，在平面直角坐标系中，以点为顶点任作一直角，使其两边分别与轴、轴

    的正半轴交于点、，连接，过点作于点，设点的横坐标为，的长为，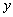

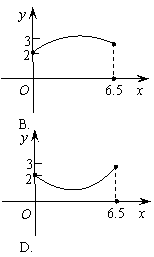
    则下列图象中，能表示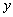与的函数关系的图象大致是（   ）

     


    查看答案和解析>>

    科目：初中数学 来源： 题型：


     解不等式组.

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    一盒子内放有只有颜色不同的2个红球、3个白球和4个黑球，搅匀后任意摸出1个球是黑球的概率为（　　）

    A．               B．               C．               D．

    查看答案和解析>>

    科目：初中数学 来源： 题型：


    问题：在中，，∠A=100°，BD为∠B 的平分线，探究AD、BD、BC之间的数量关系.

    请你完成下列探究过程：

    （1）观察图形，猜想AD、BD、BC之间的数量关系为                         .

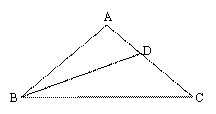    （2）在对（1）中的猜想进行证明时，当推出∠ABC=∠C=40°后，可进一步推出∠ABD=∠DBC=           度.

    （3）为了使同学们顺利地解答本题（1）中的猜想，小强同学提供了一种探究的思路：在BC上截取BE=BD，连接DE,在此基础上继续推理可使问题得到解决.你可以参考小强的思路，画出图形，在此基础上对（1）中的猜想加以证明.也可以选用其它的方法证明你的猜想.

    查看答案和解析>>

    同步练习册答案