
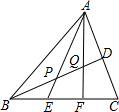
 如图,在△ABC中,E,F是边BC上的两个三等分点,D是AC的中点,BD分别交AE,AF,AC于P,Q,D,求BP:PQ:QD.
如图,在△ABC中,E,F是边BC上的两个三等分点,D是AC的中点,BD分别交AE,AF,AC于P,Q,D,求BP:PQ:QD. 分析 过D作DG∥BC,交AE于G,AH于H,根据三角形中位线定理得到CF=2DH,得到QB=4DQ,BP=PD,得到BP、PQ与DQ的关系,求比即可.
解答 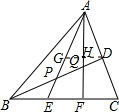 解:过D作DG∥BC,交AE于G,AH于H,
解:过D作DG∥BC,交AE于G,AH于H,
∵D为AC中点,
∴DH是△AFC的中位线,
∴DH=$\frac{1}{2}$CF,CF=2DH,
∵BE=EF=CF,
∴BF=2CF=4DH,
∵DG∥BC,
∴$\frac{DQ}{QB}$=$\frac{DH}{BF}$=$\frac{1}{4}$,
∴QB=4DQ,
∵DG是△AEC的中位线,
∴DG=$\frac{1}{2}$CE=EF=BE,
∵DG∥BC,
∴BP=PD,
∴PQ=1.5DQ,BP=2.5DQ,
∴BP:PQ:QD=5:3:2.
点评 本题考查的是平行线分线段成比例定理和三角形中位线定理,灵活运用定理、找准对应关系是解题的关键.


科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
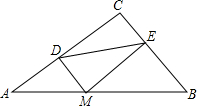 如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为$\frac{12}{5}$.
如图,在Rt△ABC中,∠C=90°,BC=3,AC=4,M为斜边AB上一动点,过M作MD⊥AC,过M作ME⊥CB于点E,则线段DE的最小值为$\frac{12}{5}$.查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:填空题
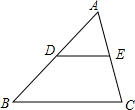 如图,△ABC中,点DE分别是ABAC的中点,则下列结论:
如图,△ABC中,点DE分别是ABAC的中点,则下列结论:查看答案和解析>>
科目:初中数学 来源: 题型:填空题
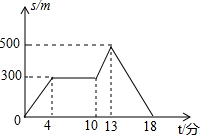 星期日晚饭后,小红从家里出去散步,如图所示,描述了她散步过程中离家的距离s(m)与散步所用的时间t(min)之间的函数关系,该图象反映的过程是:小红从家出发,到了一个公共阅报栏,看了一会报后,继续向前走了一段,在邮亭买了一本杂志,然后回家了.依据图象回答下列问题
星期日晚饭后,小红从家里出去散步,如图所示,描述了她散步过程中离家的距离s(m)与散步所用的时间t(min)之间的函数关系,该图象反映的过程是:小红从家出发,到了一个公共阅报栏,看了一会报后,继续向前走了一段,在邮亭买了一本杂志,然后回家了.依据图象回答下列问题查看答案和解析>>
科目:初中数学 来源: 题型:解答题
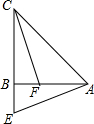 在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF.
在△ABC中,AB=CB,∠ABC=90°,E为CB延长线上一点,点F在AB上,且AE=CF.查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com