
分析 (1)设挂式空调每台的采购价是x元,电风扇每台的采购价是y元,根据采购价格=单价×数量,可列出关于x、y的二元一次方程组,解方程组即可得出结论;
(2)设再购进空调a台,则购进风扇(70-a)台,根据采购价格=单价×数量,可列出关于a的一元一次不等式,解不等式即可得出结论.
解答 解:(1)设挂式空调每台的采购价是x元,电风扇每台的采购价是y元,
根据题意,得$\left\{\begin{array}{l}{8x+20y=17400}\\{10x+30y=22500}\end{array}\right.$,
解得$\left\{\begin{array}{l}{x=1800}\\{y=150}\end{array}\right.$.
答:挂式空调每台的采购价是1800元,电风扇每台的采购价是150元.
(2)设再购进空调a台,则购进风扇(70-a)台,
由已知,得1800a+150(70-a)≤30000,
解得:a≤11$\frac{9}{11}$,
故该经营业主最多可再购进空调11台.
点评 本题考查了二元一次方程组的应用以及解一元一次不等式,解题的关键是:(1)列出关于x、y的二元一次方程组;(2)列出关于a的一元一次不等式.本题属于基础题,难度不大,解决该题型题目时,根据数量关系列出方程(方程组或不等式)是关键.


 手拉手全优练考卷系列答案
手拉手全优练考卷系列答案科目:初中数学 来源: 题型:选择题
| A. | 0既不是正数,也不是负数 | |
| B. | 若仓库运进货物5t记作+5t,那么运出货物5t记作-5t | |
| C. | 0是自然数,也是整数,也是有理数 | |
| D. | 一个有理数不是正数,那它一定是负数 |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
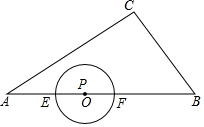 如图,在Rt△ABC中,∠C=90°,BC=3,∠A=30°,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也运动到点B时停止.在点E、F运动过程中,以EF为直径作⊙O.设点E运动的时间为t秒.
如图,在Rt△ABC中,∠C=90°,BC=3,∠A=30°,点P在AB上,AP=2.点E、F同时从点P出发,分别沿PA、PB以每秒1个单位长度的速度向点A、B匀速运动,点E到达点A后立刻以原速度沿AB向点B运动,点F运动到点B时停止,点E也运动到点B时停止.在点E、F运动过程中,以EF为直径作⊙O.设点E运动的时间为t秒.查看答案和解析>>
科目:初中数学 来源: 题型:解答题

查看答案和解析>>
科目:初中数学 来源: 题型:选择题
| A. | (-$\sqrt{3}$,1) | B. | ($\sqrt{3}$,-1) | C. | (-1,$\sqrt{3}$) | D. | (-1,-$\sqrt{3}$) |
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
科目:初中数学 来源: 题型:解答题
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com