
【题目】解方程:(1)2x-5=3x+2;
(2)3(x+2)-2(2x-3)=12;
(3) ![]() -
-![]() =1.
=1.
科目:初中数学 来源: 题型:
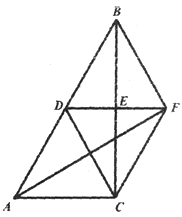
【题目】如图,在△ABC中,∠ACB=90°,CD为AB边上的中线,过点D作DE⊥BC于E,过点C作AB的平行线与DE的延长线交于点F,连接BF,AF.
(1)求证:四边形BDCF为菱形:
(2)若四边形BDCF的面积为24,CE:AC=2:3,求AF的长.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知P点是∠AOB平分线上一点,PC⊥OA,PD⊥OB,垂足为C、D.
(1)求证:∠PCD=∠PDC;
(2)求证:OP是线段CD的垂直平分线.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,已知OP平分∠AOB,∠AOB=60°,CP=2,CP∥OA,PD⊥OA于点D,PE⊥OB于点E.如果点M是OP的中点,则DM的长是( ) 
A.2
B.![]()
C.![]()
D.![]()
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,某景区内的环形路是边长为1000米的正方形ABCD.现有1号、2号两辆游览车分别从出口A和景点C同时出发,1号车顺时针、2号车逆时针沿环形路连续循环行驶,供游客随时免费乘车(上、下车的时间忽略不计),两车速度均为200米/分,设行驶时间为t分,解决下列问题:
(1)当0≤t≤10时,分别写出1号车、2号车在左半环线离出口A的路程(用含t的代数式表示);
(2)当0≤t≤10时,求当两车相距的路程是400米时的t值;
(3)当t为何值时,1号车第三次恰好经过景点C?并直接写出这一段时间内它与2号车相遇的次数.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,AC=3,点D是BC上一动点,连结AD,将△ACD沿AD折叠,点C落在点C′,连结C′D交AB于点E,连结BC′.当△BC′D是直角三角形时,DE的长为 . 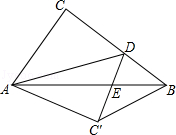
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图所示,回答下列问题:
(1)比较∠FOD与∠FOE的大小;
(2)借助三角板比较∠DOE与∠BOF的大小;
(3)借助量角器比较∠AOE与∠DOF的大小.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图1,在平面直角坐标系中,直线y=﹣x+1与抛物线y=ax2+bx+c(a≠0)相交于点A(1,0)和点D(﹣4,5),并与y轴交于点C,抛物线的对称轴为直线x=﹣1,且抛物线与x轴交于另一点B.
(1)求该抛物线的函数表达式;
(2)若点E是直线下方抛物线上的一个动点,求出△ACE面积的最大值;
(3)如图2,若点M是直线x=﹣1的一点,点N在抛物线上,以点A,D,M,N为顶点的四边形能否成为平行四边形?若能,请直接写出点M的坐标;若不能,请说明理由.
查看答案和解析>>
科目:初中数学 来源: 题型:
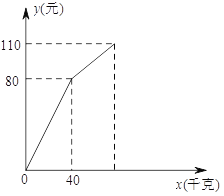
【题目】小明在暑假社会实践活动中,以每千克![]() 元的价格从批发市场购进若干千克西瓜市场上去销售,在销售了
元的价格从批发市场购进若干千克西瓜市场上去销售,在销售了![]() 千克之后,余下的打折全部售完.销售金额
千克之后,余下的打折全部售完.销售金额![]() (元)售出西瓜的千克数
(元)售出西瓜的千克数![]() (千克)之间的关系如图所示.请你根据图像提供的信息完成以下问题:
(千克)之间的关系如图所示.请你根据图像提供的信息完成以下问题:
(![]() )求降价前销售金额
)求降价前销售金额![]() (元)与售出西瓜
(元)与售出西瓜![]() (千克)之间的关系;
(千克)之间的关系;
(![]() )小明这次社会实践活动赚了多少钱?
)小明这次社会实践活动赚了多少钱?
(![]() )若要使这次活动赚
)若要使这次活动赚![]() 元钱,问余下的西瓜应打几折销售完?
元钱,问余下的西瓜应打几折销售完?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com