练习册

  • 练习册
  • 试题
    精英家教网 > 初中数学 > 题目详情
    10．计算：|1-$\sqrt{8}$|-2sin45°+（$\frac{1}{2}$）-2+$\root{3}{-8}$．

    分析 原式利用绝对值的代数意义，特殊角的三角函数值，负整数指数幂法则，以及立方根定义计算即可得到结果．

    解答 解：原式=2$\sqrt{2}$-1-2×$\frac{\sqrt{2}}{2}$+4-2=$\sqrt{2}$+1．

    点评 此题考查了实数的运算，负整数指数幂，熟练掌握运算法则是解本题的关键．

    练习册系列答案
    年级 高中课程 年级 初中课程
    高一 高一免费课程推荐！ 初一 初一免费课程推荐！
    高二 高二免费课程推荐！ 初二 初二免费课程推荐！
    高三 高三免费课程推荐！ 初三 初三免费课程推荐！
    相关习题

    科目：初中数学 来源： 题型：解答题

    20．如图，①，A（4，0），C（0，n）分别是x和y轴上的点，n＞0，以OA，OC为边在第一象限内作矩形OABC，对角线OB，AC，交于点D双曲线y=$\frac{k}{x}$（x＞0，k＞0）交边BC于G，交边AB于H．
    （1）设直线AC的函数关系式为y=qx+p，请用含n的代数式表示q和p；
    （2）求证：AB•BG=BC•BH；
    （3）如图②，若上述双曲线经过点D，判断点D是否是双曲线与直线AC唯一的交点，请说明理由．

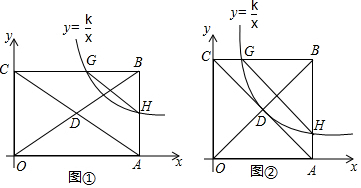
    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

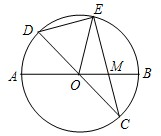    1． 已知：如图，在半径我4的⊙O中，AB、CD是两条直径，M我OB的中点，CM的延长线交⊙O于点E，且EM＞MC，连接DE，DE=$\sqrt{15}$．
    （1）求证：△AMC∽△EMB；
    （2）求EM的长；
    （3）求sin∠EOB的值．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    18．被誉为“中原第一高楼”的郑州会展宾馆坐落在风景如画的如意湖上，这座外形酷似嵩岳寺塔的摩天建筑，是郑州市乃至河南省的新“名片”，在其观光层，可以北望黄河，南眺嵩山，小华想测量郑州会展宾馆AB的高度，想到了如下方法：在湖对岸选择一条基线MN，在直线MN上取点D、C、E，测得∠BDC=30°，∠BEC=45°，仰角∠ACB=80°，且DE=135m，其它请看下面的提示，请你帮助小华算出AB的高度（参考数据：tan80°≈5.67，$\sqrt{3}$≈1.73，结果精确到十位）

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

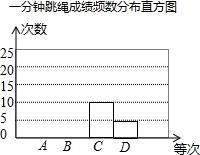    5．今年，合肥市中考体育分数再次增加5分，由去年的50分增加到55分．为备战体育中考，张勇同学就自己平时1分钟跳绳的训练成绩，做了统计，并将训练成绩绘出了如图的频数分布表和频数分布直方图（不完整）（规定：1分钟跳绳120个以下成绩为D等；120-140个为C等；140-160个为B等，160个以上为A等）
    根据以上信息，解答下列问题：
    （1）张勇同学一共记录了50次平时测试的成绩；
    （2）补全频数分布表和频数分布直方图；
    （3）张勇同学从篮球运动、足球运球、掷实心球、坐位体前屈、1分钟跳绳、立定跳远等六个项目中任选两项作为自己的考试项目，求恰好含有1分钟跳绳项目的概率．
    　　 一分钟跳绳成绩分布表
    成绩等次频数（人）频率
    D50.1
    C100.2
    B250.5
    A100.2
    合计501.00

    查看答案和解析>>

    科目：初中数学 来源： 题型：选择题

    15．实数a在数轴上的位置如图所示，则a的值可能为（　　）
    A．-4B．-3C．-2D．1

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    2．计算：（-π）0×$\root{3}{-8}$×2-1+|-2018|．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

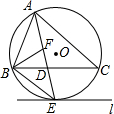    19．如图，△ABC是⊙O的内接三角形，∠BAC的角平分线AE交⊙O于点E，交BC于点D，过点E作直线l∥BC．
    （1）判断直线l与⊙O的位置关系，并说明理由；
    （2）若在AE上取一点F使BE=EF，求证：BF是∠ABC的平分线；
    （3）在（2）的条件下，若DE=3，DF=2，求AF的长．

    查看答案和解析>>

    科目：初中数学 来源： 题型：解答题

    20．如图，抛物线与x轴交于A（x1，0）、B（x2，0）两点，且x1＜x2与y轴交于点C（0，4），其中x1，x2是方程x2-4x-12=0的两个根．
    （1）求抛物线的解析式；
    （2）点M是线段AB上的一个动点，过点M作MN∥BC，交AC于点N，连结CM，当△CMN的面积最大时，求点M的坐标；
    （3）点D（4，k）在（1）中抛物线上，点E为抛物线上一动点，在x轴上是否存在点F，使以A、D、E、F为顶点的四边形是平行四边形？如果存在，直接写出所有满足条件的点F的坐标；若不存在，请说明理由．

    查看答案和解析>>

    同步练习册答案