
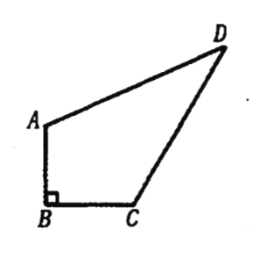
【题目】如图,某住宅小区在施工过程中留下了一块空地(图中的四边形![]() ),经测量,在四边形
),经测量,在四边形![]() 中,
中,![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
(1)若连接![]() ,则
,则![]() 是直角三角形吗?为什么?
是直角三角形吗?为什么?
(2)小区为美化环境,欲在空地上铺草坪,已知草坪每平方米150元,试问铺满这块空地共需花费多少元?
科目:初中数学 来源: 题型:
【题目】某奶粉每袋的标准质量为![]() 克,在质量检测中,超过标准质量
克,在质量检测中,超过标准质量![]() 克记作
克记作![]() 克,若低于标准质量
克,若低于标准质量![]() 克以上(不包括
克以上(不包括![]() 克)的,则这袋奶粉不合格,现在抽取
克)的,则这袋奶粉不合格,现在抽取![]() 袋样品进行质量检测,结果如下(单位:克):
袋样品进行质量检测,结果如下(单位:克):
袋号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
记作(克) |
|
|
|
|
|
|
|
|
|
|
(1)这![]() 袋奶粉中有哪几袋不合格?
袋奶粉中有哪几袋不合格?
(2)质量最少的是哪袋?它的实际质量是多少?
(3)这![]() 袋奶粉的平均质量是多少?
袋奶粉的平均质量是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
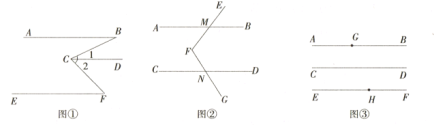
【题目】探究:如图①, ![]() ,试说明
,试说明![]() .下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.
.下面给出了这道题的解题过程,请在下列解答中,填上适当的理由.
解: ∵![]() .(已知)
.(已知)
∴ ![]() .( )
.( )
同理可证, ![]() .
.
∵ ![]() ,
,
∴![]() .( )
.( )
应用:如图②, ![]() ,点
,点![]() 在
在![]() 之间,
之间,![]() 与
与![]() 交于点
交于点![]() ,
,![]() 与
与![]() 交于点
交于点![]() .若
.若![]() ,
,![]() ,则
,则![]() 的大小为_____________度.
的大小为_____________度.
拓展:如图③,直线![]() 在直线
在直线![]() 之间,且
之间,且![]() ,点
,点![]() 分别在直线
分别在直线![]() 上,点
上,点![]() 是直线
是直线![]() 上的一个动点,且不在直线
上的一个动点,且不在直线![]() 上,连结
上,连结![]() .若
.若![]() ,则
,则![]() =________度.
=________度.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某项工程由甲乙两队分别单独完成,则甲队用时是乙队的1.5倍:若甲乙两队合作,则需12天完成,请问:
(1)甲,乙两队单独完成各需多少天;
(2)若施工方案是甲队先单独施工![]() 天,剩下工程甲乙两队合作完成,若甲队施工费用为每天1.5万元,乙队施工费为每天3.5万元求施工总费用
天,剩下工程甲乙两队合作完成,若甲队施工费用为每天1.5万元,乙队施工费为每天3.5万元求施工总费用![]() (万元)关于施工时间
(万元)关于施工时间![]() (天)的函数关系式
(天)的函数关系式
(3)在(2)的方案下,若施工期定为15~18天内完成(含15和18天),如何安排施工方案使费用最少,最少费用为多少万元?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】初三年级学习压力大,放学后在家自学时间较初一、初二长,为了解学生学习时间,该年级随机抽取25%的学生问卷调查,制成统计表和扇形统计图,请你根据图表中提供的信息回答下列问题:
学习时间(h) | 1 | 1.5 | 2 | 2.5 | 3 | 3.5 |
人数 | 72 | 36 | 54 | 18 |
(1)初三年级共有学生_____人.
(2)在表格中的空格处填上相应的数字.
(3)表格中所提供的学生学习时间的中位数是_____,众数是_____.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如果一元一次方程的根是一元一次不等式组的解,则称该一元一次方程为该不等式组的关联方程
(1)在方程①3x﹣1=0,②x﹣(3x+1)=﹣7中,不等式组![]() 的关联方程是 ;(填序号)
的关联方程是 ;(填序号)
(2)若不等式组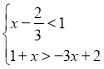 的一个关联方程的解是整数,则这个关联方程可以是 ;(写出一个即可)
的一个关联方程的解是整数,则这个关联方程可以是 ;(写出一个即可)
(3)若方程10﹣3x=2x,1+x=2(x﹣1)都是关于x的不等式组![]() 的关联方程,求出m的取值范围.
的关联方程,求出m的取值范围.
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,在正方形ABCD中,点E,F分别在边BC,CD上,且BE=CF.连接AE,BF,AE与BF交于点G.下列结论错误的是( )
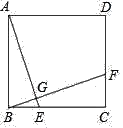
A. AE=BF B. ∠DAE=∠BFC
C. ∠AEB+∠BFC=90° D. AE⊥BF
查看答案和解析>>
科目:初中数学 来源: 题型:
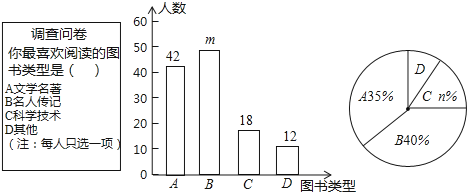
【题目】为了培养学生的阅读习惯,某校开展了“读好书,助成长”系列活动,并准备购置一批图书,购书前 ,对学生喜欢阅读的图书类型进行了抽样调查,并将调查数据绘制成两幅不完整的统计图,如图所示,根据统计图所提供的信息,回答下列问题:
(1)本次调查共抽查了 名学生,两幅统计图中的m= ,n= .
(2)已知该校共有960名学生,请估计该校喜欢阅读“A”类图书的学生约有多少人?
(3)学校要举办读书知识竞赛,七年(1)班要在班级优胜者2男1女中随机选送2人参赛,求选送的两名参赛学生为1男1女的概率是多少?
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,AB是⊙O的直径,弦CD⊥AB,垂足为H,连结AC,过![]() 上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
上一点E作EG∥AC交CD的延长线于点G,连结AE交CD于点F,且EG=FG,连结CE.
(1)求证:△ECF∽△GCE;
(2)求证:EG是⊙O的切线;
(3)延长AB交GE的延长线于点M,若tanG=![]() ,AH=
,AH=![]() ,求EM的值.
,求EM的值.

查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com