
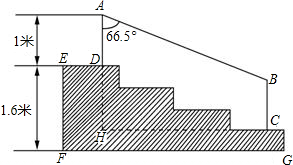
 66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30)
66.5°≈0.92,cos66.5°≈0.40,tan66.5°≈2.30) 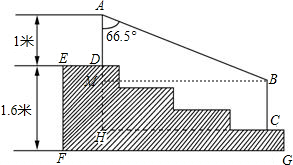 解:由图可知,台阶有4节,DH占了3节,而且还知道EF的高度,所以可以很容易得出DH:DH=1.6×
解:由图可知,台阶有4节,DH占了3节,而且还知道EF的高度,所以可以很容易得出DH:DH=1.6×| 3 |
| 4 |
| AM |
| cos66.5° |
| 1.2 |
| 0.40 |


科目:初中数学 来源: 题型:

查看答案和解析>>
科目:初中数学 来源: 题型:
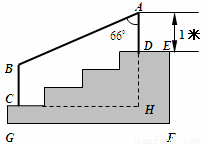
 杆AD和BC(杆子的底端分别为D,C),且∠DAB=66°.
杆AD和BC(杆子的底端分别为D,C),且∠DAB=66°.查看答案和解析>>
科目:初中数学 来源:2013年浙江省杭州市西湖区中考一模数学试卷(带解析) 题型:解答题
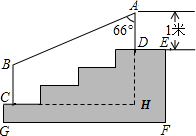
某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶,每级小台阶都为0.4米.现要做一个不锈钢的扶手AB及两根与FG垂直且长均为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且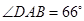 .
.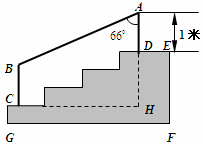
(1)求点D与点C的高度差DH的长度;
(2)求所用不锈钢材料的总长度(即AD+AB+BC).
(结果精确到0.1米.参考数据: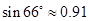 ,
,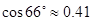 ,
,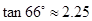 )
)
查看答案和解析>>
科目:初中数学 来源:2013年浙江省杭州市西湖区中考一模数学试卷(解析版) 题型:解答题
某学校体育场看台的侧面如图阴影部分所示,看台有四级高度相等的小台阶,每级小台阶都为0.4米.现要做一个不锈钢的扶手AB及两根与FG垂直且长均为l米的不锈钢架杆AD和BC(杆子的底端分别为D,C),且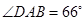 .
.
(1)求点D与点C的高度差DH的长度;
(2)求所用不锈钢材料的总长度(即AD+AB+BC).
(结果精确到0.1米.参考数据: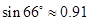 ,
,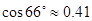 ,
,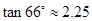 )
)
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com