
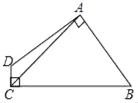
【题目】如图,四边形ABCD中,AB=AD,AC=5,∠DAB=∠DCB=90°,则四边形ABCD的面积为_____.
【答案】12.5
【解析】
过A作AE⊥AC,交CB的延长线于E,判定△ACD≌△AEB,即可得到△ACE是等腰直角三角形,四边形ABCD的面积与△ACE的面积相等,根据S△ACE=![]() ×5×5=12.5,即可得出结论.
×5×5=12.5,即可得出结论.
如图,过A作AE⊥AC,交CB的延长线于E,
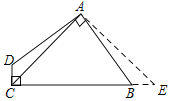
∵∠DAB=∠DCB=90°,
∴∠D+∠ABC=180°=∠ABE+∠ABC,
∴∠D=∠ABE,
又∵∠DAB=∠CAE=90°,
∴∠CAD=∠EAB,
又∵AD=AB,
∴△ACD≌△AEB(ASA),
∴AC=AE,即△ACE是等腰直角三角形,
∴四边形ABCD的面积与△ACE的面积相等,
∵S△ACE=![]() ×5×5=12.5,
×5×5=12.5,
∴四边形ABCD的面积为12.5,
故答案为12.5.


科目:初中数学 来源: 题型:
【题目】在△ABC中,∠BAC=100°,∠ABC=∠ACB,点D在直线BC上运动(不与点B、C重合),点E在射线AC上运动,且∠ADE=∠AED,设∠DAC=n.
(1)如图(1),当点D在边BC上时,且n=36°,则∠BAD= _________,∠CDE= _________.
(2)如图(2),当点D运动到点B的左侧时,其他条件不变,请猜想∠BAD和∠CDE的数量关系,并说明理由.
(3)当点D运动到点C的右侧时,其他条件不变,∠BAD和∠CDE还满足(2)中的数量关系吗?请画出图形,并说明理由.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,Rt△AOB的顶点O与原点重合,直角顶点A在x轴上,顶点B的坐标为(4,3),直线![]() 与x轴、y轴分别交于点D、E,交OB于点F.
与x轴、y轴分别交于点D、E,交OB于点F.
(1)写出图中的全等三角形及理由;
(2)求OF的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】如图,为了测量楼的高度,自楼的顶部A看地面上的一点B,俯角为30°,已知地面上的这点与楼的水平距离BC为30m,那么楼的高度AC为m(结果保留根号).
查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】一节数学课上,老师布置了一道课堂练习:“如图,在△ABC中,∠B=∠C,求证:AB=AC“,小明发现,他取BC的中点D,连接AD后,无法证明△ABD≌△ACD,故举手提问老师,老师听了他的困惑,告诉他只要再作两条垂线段就可以证明了,你知道如何继续证明吗?请你写下完整的证明过程.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】图①是一张∠AOB=45°的纸片折叠后的图形,P、Q分别是边OA、OB上的点,且OP=2cm.将∠AOB沿PQ折叠,点O落在纸片所在平面内的C处(点C在∠AOB的内部或一边上).
(1)当PC∥QB时,OQ= cm.
(2)当折叠后重叠部分为等腰三角形时,画出示意图,写出OQ的长.

查看答案和解析>>
科目:初中数学 来源: 题型:
【题目】某商场计划购进A,B两种型号的手机,已知每部A型号手机的进价比每部B型号手机进价多500元,每部A型号手机的售价是2500元,每部B型号手机的售价是2100元.
(1)若商场用50000元共购进A型号手机10部,B型号手机20部,求A、B两种型号的手机每部进价各是多少元?
(2)为了满足市场需求,商场决定用不超过7.5万元采购A、B两种型号的手机共40部,且A型号手机的数量不少于B型号手机数量的2倍.
①该商场有哪几种进货方式?
②该商场选择哪种进货方式,获得的利润最大?
查看答案和解析>>
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com